流函式
 軸對稱流動
軸對稱流動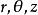 軸對稱流動
軸對稱流動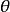 軸對稱流動
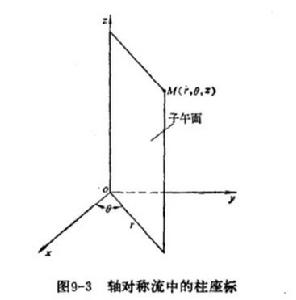
軸對稱流動我們取對稱軸為柱坐標系( )和oz軸。則流動情況與坐標 無關,且許多情況下v=0.在軸對稱流動 中,不可壓縮流體穩定流動的連續性方程可寫成柱坐標形式得到:
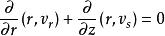 軸對稱流動
軸對稱流動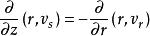 軸對稱流動
軸對稱流動或流線微分方程是:
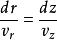 軸對稱流動
軸對稱流動其全微分函式可寫做:
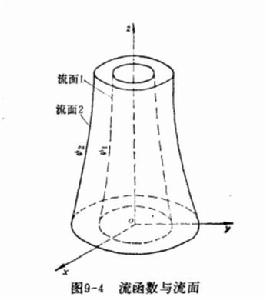 軸對稱流動
軸對稱流動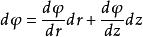 軸對稱流動
軸對稱流動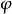 軸對稱流動
軸對稱流動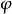 軸對稱流動
軸對稱流動在一流線上, 是常值,故稱 為流函式。由此可以推知,在軸對稱流動中,流函式在流線圍繞對稱軸轉動所構成的曲面(即流面)上保持常數。不同的常數代表不同流線及對應的流面。
研究情況
軸對稱流動最重要的情形是在直管彗中的流動,這種流動的速度剖面是拋物線型的.很早以前,Th Sexl就研究了這種流動的穩定性,他未能發現任何不穩定現象,但是他也沒有能夠證明對所有的Reynolds數這種流動都是穩定的.經過一段時間以後,J,Pret sch成功地證明了這種拋物線型速度剖面的穩定性可以歸結為平面Couette流動(純剪下流動)的穩定性.因為平面Couette流在所有的Reynolds數下都是穩定的,所以對圓管中速度剖面是拋物線型的流動,這個結論也是成立的。G.M.Corcoa和J.R.Sellars以及幾位當前正在研究這個問題的人都得到了同樣的結論,最後Th.Sexl和K.Splelberg再次證實了這個結論。由於下列兩個方面的原因,這個結論是十分令人吃驚的.第一、圓管中的流動的的確確發生轉動。第二,同樣是拋物線型速度剖面,小擾動可以使槽中的流動變得不穩定,但是卻不能使圓管中的流動失穩,這一點是很難想像的。由於這些原因,人們試圖從理論和實驗兩方面進一步研究這個問題。
套用實例
軸對稱流的一些重要的實用例子有:
1.繞超音速飛機的機身、火箭或衝壓發動機的流動。
2.繞彈體的流動。
3.在圓截面管道、噴管和擴壓器里的流動等。

