理論
超前補償器及滯後補償器都會在開環傳遞函式中增加極點-零點對,超前補償器及滯後補償器在s域下的的傳遞函式如下:
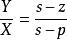 超前-滯後補償器
超前-滯後補償器其中
X為補償器的輸入
Y為輸出
s為複數的拉普拉斯變換變數
z為零點頻率
p為極點頻率
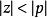 超前-滯後補償器
超前-滯後補償器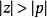 超前-滯後補償器
超前-滯後補償器一般而言零點及極點都是負數,也就是在複平面上的左半平面。若是超前補償器, ,其相位為超前的,若是滯後補償器 ,其相位為落後。
超前-滯後補償器是由一個超前補償器和滯後補償器串接而得。整體的傳遞函式如下
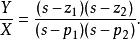 超前-滯後補償器
超前-滯後補償器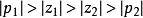 超前-滯後補償器
超前-滯後補償器一般而言 ,其中 z和 p是超前補償器的零點及極點,而 z和 p是滯後補償器的的零點及極點。一般超前補償器是在高頻時提供領先的相位。因此會將極點往左邊移動,加強系統的穩定性及加快回響。滯後補償器在低頻時提供滯後的相位,以減少穩態誤差。
準確的零點及極點位置需視閉環回響的希望特性以及待控制系統的特性而定。不過滯後補償器的零點及極點需要靠近一些,以避免讓極點右移,會讓反應變慢甚至不穩定。因為滯後補償器的主要目的是要調整低頻的特性,因此其零點與極點也需要靠近原點。
實現
模擬及數字的控制系統都可以加上超前-滯後補償器,實現的方式不同,但其背後的原理都是一樣的。其傳遞函式已經過調整,以和輸入有關的項的和,以及輸入及輸出的積分項的和組成
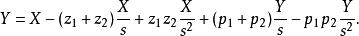 超前-滯後補償器
超前-滯後補償器在模擬控制系統中,積分器很貴,因此會設法減少需要用到的積分器:
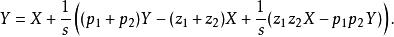 超前-滯後補償器
超前-滯後補償器在模擬控制系統中,控制信號一般會是電壓或是電流(不過也可以是液壓壓力等)。 在電子式的模擬控制系統中,超前-滯後補償器是由運算放大器的網路組合成積分器或是加權和電路的組合。若是數字控制系統,運算是用數字方式來進行。
用積分方程表示傳遞函式的原因是信號的微分常會將其噪聲放大,而積分信號可以減少噪聲的影響。以數值運算的角度而言,用積分器來實現是最穩定的。
直覺的解釋
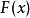 超前-滯後補償器
超前-滯後補償器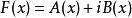 超前-滯後補償器
超前-滯後補償器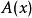 超前-滯後補償器
超前-滯後補償器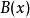 超前-滯後補償器
超前-滯後補償器若要設計超前-滯後補償器,工程師需考慮系統要改善的部分是否可分類為超前補償器、滯後補償器或是兩者的組合(超前-滯後補償器)。輸入信號的電子回響可以用網路的拉氏變換表示,也就是複數的函式,可以以二個方式來表示。複數函式 可以以下式表示 ,其中 為函式的實部,而 為函式的虛部。
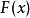 超前-滯後補償器
超前-滯後補償器 超前-滯後補償器
超前-滯後補償器網路的“相角”是 的輻角,在左半平面為 。若在所有的正負頻率下,輻角均為負值,則網路為“滯後補償器”,所有的正負頻率下,輻角均為正值,則網路為“超前補償器”。若在所有的正負頻率下,輻角有正值也有負值,則網路為“超前-滯後補償器”。
套用
超前-滯後補償器可以套用在機器人、衛星控制、汽車診斷、雷射頻率補償等套用中,是模擬控制系統及數字控制系統中的一個重要元件。
若給定待控制系統,可以用補償器來達到較理想的性能規格。P(比例)控制器、I(積分)控制器、D(微分)控制器、PI控制器、PD控制器及PID控制器都可以用來改善系統的特性(例如減小穩態誤差、共振峰值、或上升時間等)。利用補償器也可以達到類似的效果。
