簡介
 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件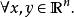 赫爾德條件
赫爾德條件數學上,稱上的實值函式適合 赫爾德條件,或稱 赫爾德連續,當存在非負常數,,使得,
 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件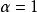 赫爾德條件
赫爾德條件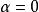 赫爾德條件
赫爾德條件這條件可以推廣至任何兩個度量空間之間的函式。稱為赫爾德條件的 指數。如果,則函式適合利普希茨條件。如果,則函式不過是有界的。
 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件由適合某個赫爾德條件的函式組成的赫爾德空間,在泛函分析有關解偏微分方程的領域有基本地位。記為某個歐幾里得空間的開集,赫爾德空間所包含的函式,是直到n階微分都適合指數的赫爾德條件。
赫爾德不等式是數學分析的一條不等式,取名自奧托·赫爾德(Otto Hölder)。這是一條揭示Lp空間的相互關係的基本不等式:
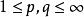 赫爾德條件
赫爾德條件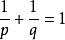 赫爾德條件
赫爾德條件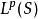 赫爾德條件
赫爾德條件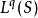 赫爾德條件
赫爾德條件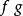 赫爾德條件
赫爾德條件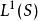 赫爾德條件
赫爾德條件設S為測度空間,,及,設f在內,g在內。則在內,且有
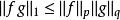 赫爾德條件
赫爾德條件。
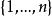 赫爾德條件
赫爾德條件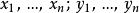 赫爾德條件
赫爾德條件若S取作附計數測度,便得赫爾德不等式的特殊情形:對所有實數(或複數),有
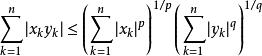 赫爾德條件
赫爾德條件。
我們稱p和q互為赫爾德共軛。
若取S為自然數集附計數測度,便得與上類似的無窮級數不等式。
當p = q = 2,便得到柯西-施瓦茨不等式。
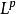 赫爾德條件
赫爾德條件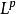 赫爾德條件
赫爾德條件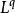 赫爾德條件
赫爾德條件赫爾德不等式可以證明空間上一般化的三角不等式,閔可夫斯基不等式,和證明空間是空間的對偶 。
備註
在赫爾德共軛的定義中,1/∞意味著零。
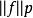 赫爾德條件
赫爾德條件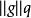 赫爾德條件
赫爾德條件如果1 ≤ p,q < ∞,那么和表示(可能無窮的)表達式:
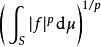 赫爾德條件
赫爾德條件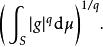 赫爾德條件
赫爾德條件以及
如果p = ∞,那么||f ||∞表示|f |的本性上確界,||g||∞也類似。
在赫爾德不等式的右端,0乘以∞以及∞乘以0意味著 0。把a > 0乘以∞,則得出 ∞ 。
證明
赫爾德不等式有許多證明,主要的想法是楊氏不等式。
如果||f ||p = 0,那么f μ-幾乎處處為零,且乘積fg μ-幾乎處處為零,因此赫爾德不等式的左端為零。如果||g||q = 0也是這樣。因此,我們可以假設||f ||p > 0且||g||q > 0。
如果||f ||p = ∞或||g||q = ∞,那么不等式的右端為無窮大。因此,我們可以假設||f ||p和||g||q位於(0,∞)內。
如果p = ∞且q = 1,那么幾乎處處有|fg| ≤ ||f ||∞ |g|,不等式就可以從勒貝格積分的單調性推出。對於p = 1和q = ∞,情況也類似。因此,我們還可以假設p, q ∈ (1,∞)。
分別用f和g除||f ||p||g||q,我們可以假設:
 赫爾德條件
赫爾德條件我們使用楊氏不等式:
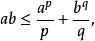 赫爾德條件
赫爾德條件對於所有非負的a和b,若且唯若ap = bq時等式成立。因此:
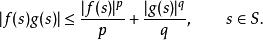 赫爾德條件
赫爾德條件兩邊積分,得:
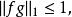 赫爾德條件
赫爾德條件這便證明了赫爾德不等式。
在p ∈ (1,∞)和||f ||p = ||g||q = 1的假設下,等式成立若且唯若幾乎處處有|f |p = |g|q。更一般地,如果||f ||p和||g||q位於(0,∞)內,那么赫爾德不等式變為等式,若且唯若存在α, β > 0(即α = ||g||q且β = ||f ||p),使得:
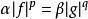 赫爾德條件
赫爾德條件。
例子
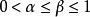 赫爾德條件
赫爾德條件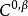 赫爾德條件
赫爾德條件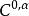 赫爾德條件
赫爾德條件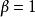 赫爾德條件
赫爾德條件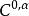 赫爾德條件
赫爾德條件如果,那么所有赫爾德連續函式都是赫爾德連續的。這也包括了(這裡需要集合是有界的),所以所有利普希茨連續函式都是赫爾德連續。
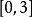 赫爾德條件
赫爾德條件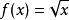 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件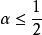 赫爾德條件
赫爾德條件 赫爾德條件
赫爾德條件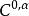 赫爾德條件
赫爾德條件在上定義函式,不是利普希茨連續;但對,是赫爾德連續。
