貝葉斯預測模型的概述
貝葉斯預測模型是運用貝葉斯統計進行的一種預測.貝葉斯統計不同於一般的統計方法,其不僅利用模型信息和數據信息,而且充分利用先驗信息。
托馬斯·貝葉斯(Thomas Bayes)的統計預測方法是一種以動態模型為研究對象的時間序列預測方法。在做統計推斷時,一般模式是:
先驗信息+總體分布信息+樣本信息→後驗分布信息
可以看出貝葉斯模型不僅利用了前期的數據信息,還加入了決策者的經驗和判斷等信息,並將客觀因素和主觀因素結合起來,對異常情況的發生具有較多的靈活性。這裡以美國1960—2005年的出口額數據為例,探討貝葉斯統計預測方法的套用。
Bayes預測模型及其計算步驟
此處使用常均值折扣模型, 這種模型套用廣泛而且簡單,它體現了動態現行模型的許多基本概念和分析特性。
常均值折扣模型
對每一時刻t常均值折模型記為DLM{1,1,V,δ},折扣因子δ,O<δ<l定義如下:
觀測方程:μ t = μ t − 1 + ω t,ω t~N [O, W t]
狀態方程: y t = μ t + v t, v t~N [0,V]
初始信息:~N [ m0, C0]
其中μ是t時刻序列的水平, V t是觀測誤差項或噪聲項,ω t是狀態誤差項。
定理:對於每一時刻t,假設μ t − 1的後驗 分布()~N [ m t − 1, C t − 1],則μ t的先驗分布()~N [ m t − 1, R t],其中 R t = C t − 1 + W t。
推論1:()~N [ f t, Q t],其中 f t = m t − 1, Q t = R t + V。
推論2:μ t的後驗分布()~N [ m t, C t],其中 m t = m t − 1 + A t e t, C t = A T v t, A t = R t / Q t, e t = y t − f t
由於Rt=Ct-1+Wt=Ct-1/δ,故有 W − t = C t − 1(δ − 1)
其計算步驟為:
(1) R t = C − t / δ; (2) Q t = R t + V;
(3) A t = R t / Q t; (4) f t − 1 = m t − 1;
(5) e t − y t − f t − 1; (6) C t = A t V;
(7) m t − m t − 1 + A t e t
計算實例
根據The SAS System for Windows 9.0所編程式,對美國出口額 (單位:十億元)變化進行了預測。選取常均值折扣模型和拋物線回歸模型。
 貝葉斯預測
貝葉斯預測美國出口額的預測, 預測模型的初始信 息為 m0=304,Co=72,V=0.Ol,δ=0.8得到的1960—2006年的預測結果。見表2中給出了預測的部分信息(1980—2006年的預測信息)。
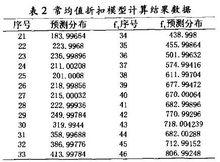 貝葉斯預測
貝葉斯預測通過The SAS System for Windows 9.0軟體回歸分析得到拋物線預測方程:
表示年份
見表3給出了1980-2006年的預測信息。
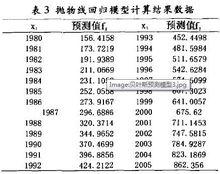 貝葉斯預測
貝葉斯預測計算結果分析
根據表l和表2對1980-2005年出口額的預測結果可知,常均值折扣模型所得結果的平均絕對百分誤差MAPE=8.1745%,而由拋物線回歸模型所得結果的平均絕對百分誤差為9.5077% 。由此可見這組數據中, 使用貝葉斯模型預測的結果更為精確。
對於隨機波動、變化相對穩定的數據,用常均值折扣模型預測是比較精確。這裡研究的貝葉斯統計預測方法,在許多領域都可能適用。在解決這類相關問題時,貝葉斯統計預測方法與傳統的預測方法相比有明顯優勢。
