變分貝葉斯估計

變分貝葉斯估計（variational Bayesian inference）是統計推斷中變分方法（variational method）的套用之一，能夠以疊代方式在給定的變分族（variational family）中對機率模型的隱變數（latent variable）後驗分布進行局部最優估計 。 變分貝葉斯估計通過平均場理論（Mean Field Theory, MFT）將隱變數的後驗按維度展開得到計算框架，並按維度疊代更新估計結果至算法收斂。基於極大後驗估計的最大期望算法（Expectation-Maximization algorithm, EM）是變分貝葉斯估計的特例之一 。 變分貝葉斯估計可以作為馬爾可夫鏈蒙特卡羅（Markov chain Monte Carlo, MCMC）的低計算量替代方法，也被套用於一些機器學習（machine learning）算法，例如變分自編碼器（variational autoencoder）的學習 。

理論

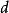變分貝葉斯估計

變分貝葉斯估計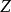

變分貝葉斯估計

給定 維觀測數據 和包含隱變數 的統計模型，由貝葉斯定理（Bayes' theorem），隱變數的後驗有如下表示：

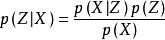變分貝葉斯估計

變分貝葉斯估計

變分貝葉斯估計的求解目標是在給定的變分族 內，找到隱變數後驗分布的最優近似，利用Kullback-Leibler散度（Kullback-Leibler divergence），該最佳化問題有如下表示 ：

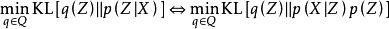變分貝葉斯估計

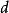變分貝葉斯估計

由KL散度的性質可知，當隱變數的後驗分布在變分族之內，例如二者均為指數族分布，則上式得到全局最優，其它情形下得到局部最優。對該最佳化問題，變分貝葉斯估計使用平均場理論（Mean Field Theory, MFT）將維的後驗分布近似為一系列一維機率分布的乘積並分別求解KL散度 ：

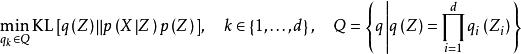變分貝葉斯估計

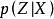變分貝葉斯估計

注意到變分貝葉斯估計通常不是無偏的，若本身不是變分族的成員，則上式中的KL散度不等於0.

算法

這裡對變分貝葉斯估計的一般計算框架進行推導。將KL散度帶入上式的最佳化問題中可有如下展開 ：

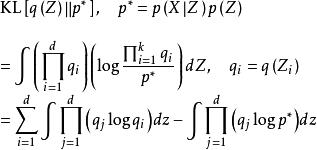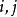變分貝葉斯估計

變分貝葉斯估計

變分貝葉斯估計

變分貝葉斯估計

變分貝葉斯估計

將式中的求和符號內的按等於和不等於分開並將不等於的部分合併為常數，則上式可化為 ：

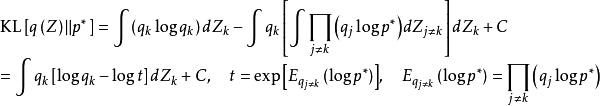變分貝葉斯估計

可知，上述積分是KL散度的定義，因此變分貝葉斯估計的最佳化問題有如下表示 ：

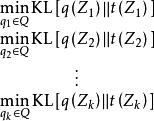變分貝葉斯估計

此即是變分貝葉斯估計的計算框架。

套用

變分貝葉斯估計可以套用於完整的貝葉斯推斷（full Bayesian inference），即對後驗分布按因子展開進行近求解。在最大期望算法（Expectation-Maximization algorithm, EM）的E步中對隱變數後驗分布的求解可以通過變分貝葉斯估計實現，形成變分貝葉斯EM（Variational Bayesian EM algorithm, VBEM） 。