隨機介質
正文
在時間和空間上特性隨機變化的電波傳播媒介。它由統計特性表征。隨機介質與許多實際問題關係密切，如對流層湍流、電離層不規則性對無線電波的散射、大氣中各種水汽凝結物對毫米波和微波傳播的影響、無線電星閃爍現象、衛星通信中的閃爍和遙感等，都與隨機介質特性有關。隨機介質大致可分成三種類型。
① 離散隨機介質：由許多隨機分布的離散質點構成，如水汽凝結物（雨、霧、雪、冰雹等）、煙霧、灰塵、海洋中的質點、紅血球細胞，以及各種聚合體和處在布朗運動狀態的其他一些質點等。對於這種隨機介質，除質點的介電特性外，質點的形狀特徵、取向和大小分布等，都是重要的統計量。
② 連續隨機介質：其介電特性即介電常數ε(r,t)或折射指數n(r,t)在空間和時間上連續地隨機變化，如對流層中的湍流、電離層中的湍流、海洋中的湍流和噴氣發動機排出的氣體等。在湍流介質中，由於湍流單元與周圍介質在溫度、壓強、濕度或電子密度上有差別，因而在折射指數上也有差別。電波通過這種介質時產生散射，如對流層散射、電離層散射等。折射指數在時間和空間上的隨機變化，造成散射波的相位、幅度和到達角的起伏。湍流的強弱用折射指數起伏強度（折射指數的方差）
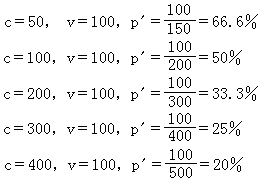表征。若在時間和空間(四維空間)中的兩點，折散指數對平均值的起伏分別為墹n(r1,t1)和墹n(r2,t2)，則其乘積的平均值
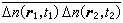稱折射起伏的相關函式。它是湍流介質中波傳播的基本參數。通過相關函式的傅立葉變換，可得到折射指數起伏的空間譜密度。若隨機介質的折射指數為非平穩隨機過程,則用結構函式 
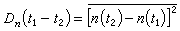代替折射指數起伏的相關函式比較方便。同樣,對局部均勻各向同性的隨機介質，也可用結構函式
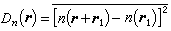描述其特徵，它類似於相關函式，由結構函式也可得到其相應的譜密度。 ③ 隨機粗糙表面：如各種起伏的地面、海面和行星表面、植被表面和不同生物介質的界面等。這種隨機介質的特性除了包括介電特性外，還與介質表面的隨機粗糙程度（相對於波長）有關。電波入射到這種介質表面時，除了在一特定方向反射電波外，還在各個方向散射電波。散射波與入射波的到達方向和極化有關。
波在隨機介質中傳播時，所發生的隨機散射場以複雜的方式互相干涉，使合成場的振幅和相位也隨機變化。因此，必須研究波的統計特性，如散射波功率中值、散射場的時間和空間相關函式或其相應的譜密度，以及散射場幅度和相位乃至其導數的機率分布等。
對於離散隨機介質，當散射體分布比較稀疏時，可用單體散射理論（略去散射體之間的相互作用，不考慮多重散射）或一階多重散射理論，並考慮散射體的尺寸分布，從而獲得總的散射場；或者用能量的輸運理論求解散射問題。若散射體較濃密時，則須考慮散射體之間的相互作用，利用較高精度的多重散射理論求解。處理連續隨機介質中的傳播問題時，首先要獲得折射指數起伏的相關函式或結構函式或其相應的空間譜密度，再求解散射截面。電波傳播研究通常遇到的是弱起伏隨機介質，其中折射指數或介電常數的隨機部分比其平均值小得多。
