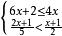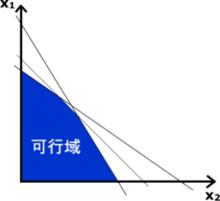解不等式組

解不等式組(solving the system of inequa-lines)就是求出給定不等式組滿足所有不等式的解的集合。

一元方程組

解一元一次不等式組的步驟：

（1）求出這個不等式組中各個不等式的解集。

（2）利用數軸求出這些不等式的解集的公共部分，即求出了這個不等式組的解集。

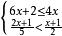解不等式組

例：解不等式組

解：由①得：6x-4x≤-2

2x≤-2

x≤-1

由②得：兩邊同時乘以10

x>-3

∴這個不等式組的解集是：-3<x≤-1

二元方程組

解一元二次不等式組的步驟：

在平面直角坐標系內畫出每個不等式的可行域，最後取這些可行域的公共部分。

解不等式組