簡介
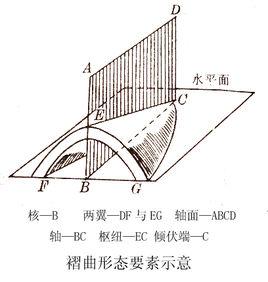
褶皺軸(folding axis)是圓柱狀褶皺的母線,是一條平行褶皺樞紐的直線,其平行自身移動的軌跡與褶皺面的幾何形態完全一致。但自然界中,許多褶皺並非圓柱狀,因此褶皺軸的這個概念只在把褶皺劃分成許多近似圓柱狀的區段,進行統計學研究時套用。
圓柱狀褶皺
圓柱狀褶皺的褶皺面可以是單一的圓柱狀的一部分,但更多的情況是由許多不同直徑共軸排列的圓柱面所構成的切面。圓柱狀褶皺的幾何性質是其褶皺面的每一部分都包含著一條與樞紐方位相同的線,這條線的方位即褶皺的方位。
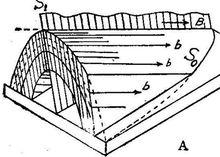 圓柱狀褶皺
圓柱狀褶皺凡不具以上特徵的褶皺統稱為非圓柱狀褶皺。非圓柱狀褶皺沒有褶皺軸,但可以有樞紐。非圓柱狀褶皺可分為許多均勻區段,每一區段可以近似地看成圓柱狀褶皺。通過逐段解析其幾何特徵,再進行綜合,可以得出整個褶皺的幾何形態及其變化。
褶皺軸與樞紐
樞紐是指單一褶皺面從一翼過渡到另一翼的彎曲部分。
顯然,褶皺軸與樞紐不同,它只具有幾何學意義而並非褶皺面上的某一具體直線,樞紐在褶皺面上是有具體位置的,但其方位與褶皺一致,因此,在圓柱狀褶皺中,褶皺的產狀可由褶皺樞紐來代表。
產狀
褶皺軸的產狀常用指向和傾伏角或用在軸面上的側伏角來確定。出露良好的小褶皺,可用羅盤直接測量褶皺的指向和傾伏角。大多數褶皺產狀是在測量兩翼產狀的基礎上,利用赤平投影方法求出的。一般採用π圖解和β圖解。
圓柱狀褶皺在赤平投影上表現為:同一褶皺面不同部位產狀投影的平面大圓交會成一點或密集在很小範圍內,而同一褶皺面不同部位的法線投影(極點)將大致沿著一平面大圓(π圓)分布。非圓柱狀褶皺的褶皺面各段的極點,在赤平投影網上的投影點相當分散,不能落在同一共同的大圓上。所以極點沿大圓(π圓)的分散程度代表了褶皺的非圓柱狀程度。非圓柱狀褶皺中的一種特殊形態稱圓錐狀褶皺,其形態可以看成是將一軸線一端固定進行鏇轉而成。在赤平投影圖上,圓錐狀褶皺的褶皺面各部位的極點呈小圓分布。