尾流簡介
 葉柵尾流
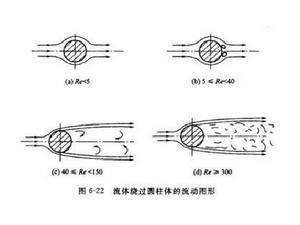
葉柵尾流尾流是指運動物體後面或物體下游的紊亂旋渦流,又稱尾跡。流體繞物體運動時,物體表面附近形成很薄的邊界層渦旋區。如果物體是象建築物或橋墩那樣的非流線型物體,流動將從物體後部表面分離,並有渦旋斷續地從物體表面脫落。這些薄邊界層或分離流渦旋區將順流而下,在物體後面形成紊亂的,充滿大大小小旋渦的尾流。如果物體是鈍體,尾流能保持很遠距離,並對處於尾流中的其他物體產生影響。
在遠離物體下游處,尾流可用邊界層理論進行分析。以下只限於討論低速湍性尾流。附圖所示為圓柱後面的平面湍性尾流流型。其中虛曲線表示尾流邊界。從圖上可以看出,由於物體的阻滯作用,尾流中速度將“虧損”(即減小)。從速度分布看,尾流象是反過來畫的射流,而且在遠離物體的下游處,尾流的虧損速度(用△ū表示)分布也具有相似性,即△ū/△ūmax≈f(y/b) 式中△ūmax為最大虧損速度。b為尾流寬度的一半;y為縱坐標。但是,尾流與射流根本不同。尾流的對流加速度比射流大得多。由邊界層方程推出的尾流方程也不一樣。H. 施利希廷根據混合長和相似性等假設,求出平面湍性尾流的解。其主要結果如下:
①尾流寬度同到物體的距離的平方根成正比;
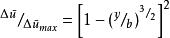 葉柵尾流
葉柵尾流②虧損速度分布為:
③尾流中心最大速度虧損同上述距離的平方根成反比。當這一距離很大時,尾流速度虧損可以忽略。
對於三維物體後面的尾流可作類似的分析。在高速尾流中應當考慮流體的可壓縮性影響。在高超聲速尾跡中則發生一系列物理化學現象,其分析方法根本不同。
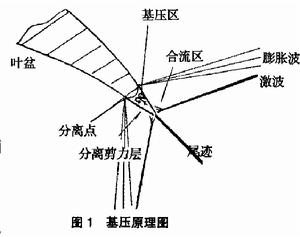
基壓對跨聲速渦輪葉柵尾跡損失影響的研究
在亞聲速氣流中,渦輪葉片的尾跡損失與附面層損失相比,通常是很小的,因此在薄尾緣研究中經常忽略了尾跡損失。然而,隨著出口馬赫數增加到聲速,損失係數將急劇增大。在跨聲速範圍內,通常損失是隨馬赫數增大而增加的。隨著損失的增大。葉片的尾跡將形成複雜的激波型式。
跨聲速渦輪尾跡損失是葉柵損失的主要部分,它大約占總損失的三分之一。跨聲速尾跡氣流是十分複雜的,必須要了解其基本的氣流流動模型。目前計算損失的方法大多是根據經驗的公式,但這個方法影響了計算損失的準確性。國外的一些研究表明:基壓(BaseerPssuer)和損失、基壓和反壓都存在著一定的關係。早在20世紀80年代初,Sieverding就開展了跨聲速葉柵基壓問題的研究,隨後英國劍橋大學Xu.L和Denton先後對基壓問題進行了比較詳細的研究。北京航空航天大學徐露在劍橋大學的博士論文“跨聲速渦輪葉片的基壓和尾跡損失”(1985年)、“四組渦輪葉片的基壓和損失”和“跨聲速渦輪葉片的尾跡損失”文章中,側重於從理論上推導葉片尾緣的激波型式和尾跡損失產生的機理,在理論分析中大多數是以簡化的圓形尾緣和三角形尾緣為基礎的。而在真實的渦輪葉片中,尾緣的型式是不同的。
Diceh等人系統地研究了在跨聲速範圍內尾緣厚度和形狀對損失的影響,然而他們沒有提供詳細的試驗數據,以致他們所給出的研究結果幾乎對了解損失的機理沒有幫助。但他們能將尾緣損失修正為尾緣厚度的線性關係。Prust和Helon完成了在亞聲速不同尾緣形狀和厚度的葉柵試驗,他們得出結論:損失是與阻力係數成正比,並與基壓成函式關係。