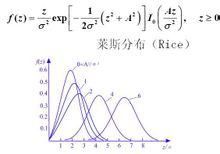
萊斯分布的概念
Stephen Rice在機率論與數理統計領域中，萊斯分布（Rice distribution或Riciandistribution）是一種連續機率分布，以美國科學家史蒂芬·萊斯（Stephen O. Rice）的名字命名。
在隨機過程里，正弦（餘弦）信號加窄帶高斯隨機信號的包絡服從萊斯分布。萊斯分布也稱作廣義瑞利分布。
機率密度函式及意義
萊斯分布的機率密度函式稱為萊斯（Rice）密度函式，函式為：
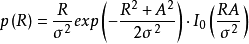萊斯分布
萊斯分布萊斯分布實際上可以理解為主信號與服從瑞利分布的多徑信號分量的和。機率密度函式公式中，R即為正弦（餘弦）信號加窄帶高斯隨機信號的包絡，參數A是主信號幅度的峰值，σ^2是多徑信號分量的功率，()是修正的0階第一類貝塞爾函式。
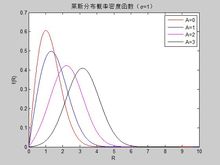萊斯分布機率密度函式K的機率密度函式如右圖所示。
萊斯分布常用參數K來描述，K定義為主信號的功率與多徑分量功率之比，即K=（A^2）/（2σ^2）。K稱作萊斯因子，由K可以完全確定萊斯分布。當A->0時，萊斯分布轉變為瑞利分布。
瑞利分布參見
