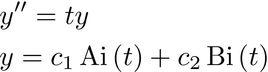概念介紹
（Ai( x)），英文名 airy function。英國英格蘭天文學家、數學家喬治·比德爾·艾里命名的特殊函式，他在1838年研究光學的時候遇到了這個函式。Ai( x)的記法是Harold Jeffreys引進的。Ai( x)與相關函式Bi( x)（也稱為艾里函式），是以下微分方程的解：
y''=xy
這個方程稱為艾里方程或斯托克斯方程。這是最簡單的二階線性微分方程，它有一個轉折點，在這一點函式由周期性的振動轉變為指數增長（或衰減）。
定義
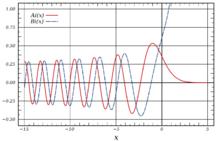艾里函式圖像對於實數 x，艾里函式由以下的積分定義： Ai(x)=1/π*∫cos(t^3/3+xt) dt (0~+∞)
把:y = Ai(x)求導，我們可以發現它滿足以下的微分方程：
y''=xy
因為這個方程有兩個線性獨立的解，所以，第二個解成為“ 第二艾里函式”。它定義為當 x趨於−∞時，振幅與Ai(x)相等，但相位與Ai(x)相差π/2的函式：
Bi(x)=1/π*∫e^(-t^3/3+xt)+sin(t^3/3+xt) dt (0~+∞)
性質
當 x趨於+∞時，艾里函式的漸近表現為：
Ai(x)~e^(-2/3*x^(3/2))/(2sqr(π)x^(1/4))
Bi(x)~e^(2/3*x^(3/2))/(sqr(π)x^(1/4))
而對於負數方向的極限，則有：
Ai(-x)~sin(2/3*x^(3/2)+π/4)/(sqr(π)x^(1/4))
Bi(-x)~cos(2/3*x^(3/2)+π/4)/(sqr(π)x^(1/4))
自變數複數時
我們可以把艾里函式的定義擴展到整個複平面：
Ai(z)=1/(2πi)*∫e^(t^3/3+zt) dt (C~∞)
其中積分路徑 C從輻角為-(1/3)π的無窮遠處的點開始，在輻角為(1/3)π的無窮遠處的點結束。此外，我們也可以用微分方程 y'' − x y = 0來把Ai( x)和Bi( x)延拓為複平面上的整函式。
以上Ai( x)的漸近公式在複平面上也是正確的，如果取主值為 x^(2/3)，且 x不在負的實數軸上。Bi( x)的公式也是正確的，只要 x位於扇形 {x∈C: |arg x| < (1/3)π−δ}內，對於某個正數δ。最後，Ai(− x)和Bi(− x)是正確的，如果 x位於扇形 {x∈C: |arg x| < (2/3)π−δ}內。
從艾里函式的漸近表現可以推出，Ai( x)和Bi( x)在負的實數軸上都有無窮多個零點。Ai( x)在複平面內沒有其它零點，而Bi( x)在扇形 {z∈C: (1/3)π < |arg z| < (1/2)π}內還有無窮多個零點。
函式關係
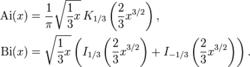艾里函式與變形貝塞爾函式的關係當自變數是正數時，艾里函式與變形貝塞爾函式之間有以下的關係：-
-
-
-
在這裡， I±1/3和 K1/3是方程 x^2* y'' + x y' − ( x^2 + 1 / 9) y = 0的解。
----
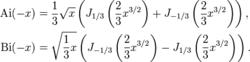艾里函式與貝塞爾函式的關係當自變數是負數時，艾里函式與貝塞爾函式之間有以下的關係：-
-
-
在這裡， J±1/3是方程 x^2* y'' + x y' + ( x^2 − 1 / 9) y = 0的解。
----
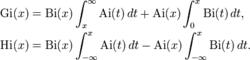Score函式Scorer函式是 y'' − x y = 1/π的解，它也可以用艾里函式來表示：
