定義
假設一個 (p+q)×(p+q)的矩陣M被分為A, B, C, D四個部分,分別是p×p、p×q、q×p以及q×q的矩陣,也就是說:
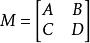 舒爾補
舒爾補並且D是可逆的矩陣。則D在矩陣中的 舒爾補是:
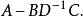 舒爾補
舒爾補這是一個 p× p的矩陣。 舒爾補得名於數學家伊賽·舒爾,後者用舒爾補來證明舒爾引理。然而,舒爾補的概念在之前就曾經被使用過。
背景
舒爾補實際上是對原來的矩陣M進行一系列的初等變換操作後得到的矩陣,其轉換矩陣是下三角矩陣:
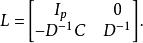 舒爾補
舒爾補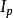 舒爾補
舒爾補其中 表示一個p×p的單位矩陣。矩陣M右乘轉換矩陣L之後,左上角就會出現舒爾補,具體的形式是:
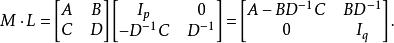 舒爾補
舒爾補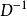 舒爾補
舒爾補因此,矩陣 M的逆,如果存在的話,可以用 以及其舒爾補(如果存在的話)來表示:
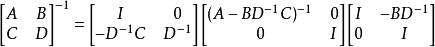 舒爾補
舒爾補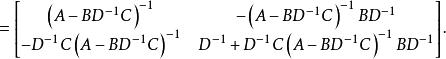 舒爾補
舒爾補當 p和 q都等於1(即 A、 B、 C和 D都是係數)時,我們可以得到一般的2 × 2的矩陣的逆矩陣表達式:
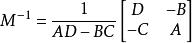 舒爾補
舒爾補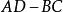 舒爾補
舒爾補這也說明了 是非零的數。
在矩陣方程求解中的套用
舒爾補很自然地可以在如下的方程組求解中發揮作用:
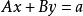 舒爾補
舒爾補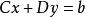 舒爾補
舒爾補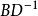 舒爾補
舒爾補其中x以及a是p維的列向量,而y以及b則是q維的列向量。矩陣A、B、C、D則同上面假設。將第二個方程左乘上矩陣 ,並將得到後的方程與第一個相減,就得到:
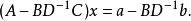 舒爾補
舒爾補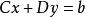 舒爾補
舒爾補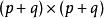 舒爾補
舒爾補因此,如果可以知道 D以及 D的舒爾補的逆矩陣,就可以解出未知量 x之後帶入第二個方程 就可以解出 y。這樣,就將 矩陣的求逆問題轉化成了分別求解一個p×p矩陣以及一個 q×q矩陣的逆矩陣的問題。這樣就大大減低了複雜度(計算量)。實際上,這要求矩陣D滿足足夠好的條件,以使得算法得以成立。
機率論和統計學中的套用
 舒爾補
舒爾補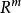 舒爾補
舒爾補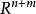 舒爾補
舒爾補假設有分別屬於 以及 的隨機列向量 X, Y,並且 中的向量對 ( X, Y)具有多維常態分配,其方差矩陣是對稱的正定矩陣
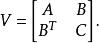 舒爾補
舒爾補那么X在Y給定時的條件方差是矩陣C在V中的舒爾補:
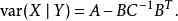 舒爾補
舒爾補