基本介紹
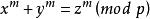舒爾定理舒爾定理是德國數學家舒爾(I.Schur，1875～1944)在1916年發表的一篇研究有限域上的費馬大定理的論文中證明的，論文的題目叫做“論同餘式 ”，這裡所說的舒爾定理是為了證明論文的主要結果而先行證明的結論。
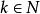舒爾定理
舒爾定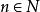理
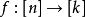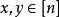舒爾定理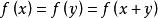
舒爾定理
舒爾定理舒爾定理(有限形式) 對任一給定的 ，存在 ，使得對[n]的任一k-染色 ，有 使 (這裡的x，y可能相等)，上述數n的最小值記為S(k)。
舒爾定理的推廣
舒爾定理是拉姆塞理論的源頭之一，雖然舒爾本人證明這個定理是為了研究別的問題，而且以後他也沒有在拉姆塞理論這一領域發表其他研究成果，但在這一理論的發展史上至少有二件大事與舒爾緊密相關。
i)在研究數論(有關於二次剩餘和二次非剩餘的分布)問題時，舒爾在1920年提出了一個猜想，這個猜想在1927年被荷蘭數學家范德瓦爾登(B.L.van der Waerden)證明為真，從而成為拉姆塞理論——也是數論——的一個著名經典定理(後來這個定理稱作范德瓦爾登定理)。
ii)舒爾指導了他的一位博士生拉多(R.Rado)寫作學位論文，在拉多的1933年的學位論文以及隨後的一系列更進一步的研究工作中，拉多證明了一個深刻的定理(後來被稱作拉多定理)，這個定理既是舒爾定理又是范德瓦爾登定理的非常深刻的推廣，它也是拉姆塞理論的經典定理之一。
這裡要介紹的是和舒爾定理的形式上很相像的一種深刻推廣，為敘述簡明，同時也為了更突出舒爾定理的定性方面，先給出舒爾定理的無限形式。
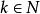舒爾定理
舒爾定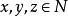理
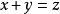舒爾定理舒爾定理(無限形式) 對任一給定的以及N的任一k-染色，一定有同色的 滿足 。
這是舒爾定理的有限形式的直接推論。
下面的這個推廣結果是20世紀60年代後至少三位數學家各自獨立地發現的，為了紀念其中已不幸天亡而又對拉姆塞理論作出傑出貢獻的一位數學家福克曼(J.Folkman，1938～1969)，我們遵從很多文獻的說法，把這一結果稱作福克曼定理。
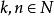舒爾定理福克曼定理 對任意給定的以及N的任一k-染色，N中一定有n元子集A，使得A中任意多個不同的數的和都同色。(更詳細地說，對A的每個非空子集X，記X中各數之和為n(x)，則所有n(X)都同色。)
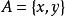舒爾定理注意，當n=2時，存在2元子集使得x，y，x+y同色就得到舒爾定理(因這裡的x，y，x+y是3個不同的數，所以結論還比舒爾定理稍強一些)。
後來發現上述福克曼定理實際上可以從拉多定理推導出來(這個推導並不簡單)，但福克曼定理仍有其價值。其中之一是福克曼定理的表述方式促使人們作進一步的探索，最著名的一個深刻推廣是欣德曼(N.Hindman)在1974年證明的下述結果：
欣德曼定理 對N的任一有限染色，N中一定有無限子集A，使得A中任意有很多個不同數之和都同色。
欣德曼定理是福克曼定理在更深層次上的推廣。一般說來，證明一定存在具有某些性質的無限子集和證明一定存在有限子集有本質性不同，欣德曼定理不能從別的存在有限子集的結論導出，證明它需要新方法，當然，它也成為進一步研究的新源頭。
最後再對福克曼定理講一個沒有解決的猜想，首先很容易證明，如果在福克曼定理中把結論中的“和”改成“積”，則定理仍成立，具體地說，有下述結論：
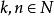舒爾定理定理(福克曼定理的乘積形式) 對任意給定的以及N的任一k-染色，N中一定有n元子集A'，使得A'中任意多個不同的數的積都同色 。
