定義
假設相變出現在臨界溫度 T處。 為研究臨界溫度附近物理量 f的行為，我們引入約化溫度
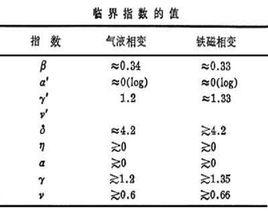
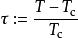臨界指數
臨界指數相變即發生於約化溫度為0時。於是，可以定義 臨界指數：
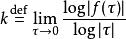臨界指數相應的冪律關係為
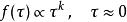臨界指數這代表了 τ→ 0時函式 f( τ)的漸近行為。更加普遍地，我們有
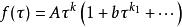臨界指數Ising類系統的平均場臨界指數
標量場（其中Ising模型是原型示例）的 臨界指數的經典Landau理論（平均場理論）值由下式給出：
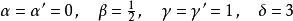臨界指數如果我們添加衍生術語將其轉化為平均場Ginzburg-Landau理論，我們得到
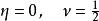臨界指數關鍵現象研究的主要發現之一是臨界點的平均場理論只有在系統的空間維數為4或更高時才是正確的（不幸的是，它排除了許多與實驗相關的情況）。該維度稱為上臨界維度。平均場理論的問題在於關鍵指數不依賴於空間維度。這導致空間維度2和3的定量差異，其中真正的臨界指數與平均場值不同。它導致空間維度1的定性差異，其中臨界點實際上不再存在，即使平均場理論仍然預測存在一個。平均場理論在質量上不正確的空間維度稱為較低的臨界維度。
實驗值
對於超流氦的相變（所謂的λ躍遷）， α的最精確測量值是-0.0127。在太空梭上測量該值以最小化樣品中的壓力差。有趣的是，這個值與蒙特卡羅和高溫膨脹技術相結合的最精確的理論確定存在顯著的不同意見。其他技術在實驗中給出了一致的結果，但不太精確。
縮放功能
根據關鍵的縮放比例，我們可以無量綱的數量重新表達所有熱力學量。足夠接近 臨界點，一切都可以根據減少量的某些比率來重新表達。
縮放函式的起源可以從重整化組中看出。關鍵點是紅外線固定點。在臨界點的足夠小的鄰域中，我們可以線性化重整化群的動作。這基本上意味著，通過一個因子重新縮放系統一個將等同於通過的係數重新縮放運算符和源欄位一個一些Δ。因此，我們可以根據重新調整的規模獨立數量重新參數化所有數量。
