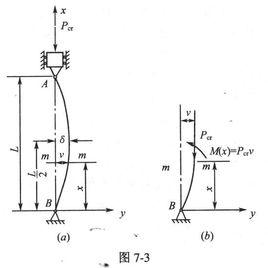
計算公式
P'=π2EI/L2 即:P等於3.14的平方乘以E 和I 與L的平方之比。
式子中P表示臨界力;E表示彈性模量; I 表示慣性矩
 臨界力Pij的大小與支承條件的關係圖
臨界力Pij的大小與支承條件的關係圖臨界力Pij的大小與下列因素有關:
1、壓桿的材料:鋼柱的P比木柱大,因為鋼柱的彈性模量E大。
2、壓桿的截面形狀與大小:截面大不易失穩,因為慣性矩大。
3、壓桿長度L:壓桿長度大,P臨界力小,易失穩。
案例解析
壓桿臨界力
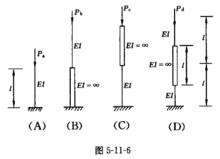
1、同一長度的壓桿,截面積及材料均相同,僅兩端支承條件不同,則一端固定,一端自由桿的臨界力最小。
2、受壓桿在下列支承情況下,若其他條件相同,臨界力最大的是兩端固定
3、受壓物件,兩端鉸支,臨界力為50kN,若將物件改為兩端固定,則其臨界力為500kN。
臨界力和歐拉公式
桿件所受壓力逐漸增加到某個限度時,壓桿將由穩定狀態轉化為不穩定狀態。這個壓力的限度稱為臨界力。它是壓桿保持直線穩定形狀時所能承受的最小壓力。
為了計算壓桿的穩定性,就要確定臨界力的大小。通過實驗和理論推導,壓桿臨界力與各個因素有關:
(1)壓桿的材料,臨界力與材料的彈性模量E成正比;
(2)壓桿橫截面的形狀和尺寸,臨界力與壓桿橫截面的軸慣性矩成正比;
(3)壓桿的長度,臨界力與長度的平方成反比;
(4)壓桿兩端的支座形式有關,用支座係數表示。
當已知壓桿的材料、尺寸和支座形式時,即可由歐拉公式求得臨界力根據歐拉公式,若要提高細長桿的穩定性,可從下列幾方面來考慮:
(1)合理選用材料:
臨界力與彈性模量E成正比。鋼材的E值比鑄鐵、銅、鋁的大,壓桿選用鋼材為宜。合金鋼的E值與碳鋼的E值近似,細長桿選用合金鋼並不能比碳鋼提高穩定性,但對短粗桿,選用合金鋼可提高工作能力。
(2)合理選擇截面形狀:
臨界力與截面的軸慣性矩成正比。應選擇大的截面形狀,如圓環形截面比圓形截面合理,型鋼截面比矩形截面合理。並且儘量使壓桿橫截面對兩個互相垂直的中性軸的慣性矩相近。
(3)減少壓桿長度:
臨界力與桿長平方成反比。在可能的情況下,減小桿的長度或在桿的中部設定支座,可大大提高其穩定性。
(4)改善支座形式:
 臨界力
臨界力臨界力與支座形式有關。固定端比鉸鏈支座的穩定性好,鋼架的立柱,其柱腳與底板的聯繫形式,能提高立柱受壓時的穩定性。
壓桿的臨界應力
歐拉公式只有在彈性範圍內才是適用的。為了判斷壓桿失穩時是否處於彈性範圍,以及超出彈性範圍後臨界力的計算問題,必須引入臨界應力及柔度的概念。
壓桿在臨界力作用下,其在直線平衡位置時橫截面上的應力稱為臨界應力,壓桿在彈性範圍內失穩時,則臨界應力為柔度與長細比的比值。
下圖為常用材料的應力計算值:
| 材 料 | |||
| A3鋼 | 304 | 1.12 | 102 |
| 優質碳鋼 | 461 | 2.568 | 95 |
| 鑄 鐵 | 332.2 | 1.454 | 70 |
| 木 材 | 28.7 | 0.190 | 80 |
分析臨界力的步驟
1、分析臨界狀態:
一般採用極端分析法,即把問題中的物理量推向極值,就會暴露出物理過程,常見的有A.發生相對滑動;B.繩子繃直;C.與接觸面脫離。
所謂臨界狀態一般是即將要發生質變時的狀態,也是未發生質變時的狀態。此時物體所處的運動狀態常見的有:A.平衡狀態;B.勻變速運動;C.圓周運動等。
2、找出臨界條件:
上述臨界狀態其對應臨界條件是:
(1)相對滑動與相對靜止的臨界條件是靜摩擦力達最大值;
(2)繩子鬆弛的臨界條件是繩中拉力為零;
(3)相互接觸的兩個物體將要脫離的臨界條件是相互作用的彈力為零。
3、列出狀態方程:
將臨界條件代到狀態方程中,得出臨界條件下的狀態方程。
4、聯立方程求解:
有些臨界問題單獨臨界條件下的狀態方程不能解決問題,則需結合其他規律聯立方程求解。