簡介
概述
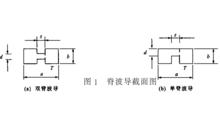脊波導截面圖脊波導分雙脊波導和單脊波導, 如圖所示。它可看作由矩形波導把寬壁彎折而成, 其中的電磁場模式與矩形波導的模式相似, 於是採用相同的模式名稱, 只是在脊棱附近由於邊緣效應使場分布受到擾動。
脊波導的主要參數有主模截止波長、脊波導單模工作頻寬、脊波導特性阻抗 脊波導功率容量、脊波導衰減。
研究背景
在現代微波工程中，為了滿足微波傳輸系統性能的某些需求，需要不斷探索和研究具有特殊截面形狀的各種新型波導。最近幾十年來，由於脊波導具有低主模截止頻率、寬頻帶和低阻抗特性，各種結構形狀的脊波導應運而生。
優點
脊波導與相同尺寸的矩形波導比較主要優點是：主模H波的截止波長較長, 對於相同的工作波長, 波導尺寸可以縮小 H模和其它高次模截止波長相隔較遠, 因此單模工作頻帶較寬, 可以達到數個倍頻程；等效阻抗較低, 因此易與低阻抗的同軸線及微帶線匹配；但脊波導承受功率比同尺寸的矩形波導低。
脊波導各參數計算
截止波長（λc）
橫向諧振條件方程
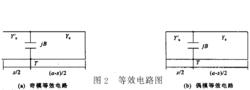圖2 等效電路圖當波導截止時, 電磁波將在兩窄邊之間來回反射, 形成諧振, 其橫向傳輸線上任何參考面的總的電納應該為零 在圖中以T面為參考面, 得到圖2的等效網路（a）、 （b） , 並由此寫出諧振方程為奇模諧振方程和偶模諧振方程。
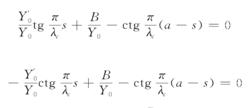奇模、偶模諧振方程矩形波導跳變引起的電納為
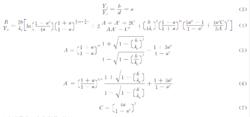矩形波導跳變引起的電納對於雙脊波導當s 為有限值時，式( 4) 只需用截止波長λc代替式中的λg即可;對於單脊波導用λc/ 2 代替式中的λg；至此，當已知脊波導的截面尺寸後，則式( 1) ~、( 2) 就是以λc為未知量的超越方程，可以數值解計算脊波導截止波長λg 通過編制計算程式，解方程獲得截止波長。
通常情況下，工程上選取的脊波導都要靠近一些標準，當雙脊波導選b/a= 0.45，單脊波導選b/a= 0. 5時 我們可以查讀工程套用曲線。並計算得雙脊波導TE模的截止波長λ 單脊波導TE模的截止波長λ
主模工作頻寬We
脊波導的主模工作頻寬定義為主模截止波長與鄰近高次模截止波長之比 對於任意脊波導，其T模截止波長總是大於T模。脊波導的理論工作頻寬為W= λ /λ。套用查表的方法可以查到當雙脊波導b/a= 0.45單脊波導b/a= 0. 5時的理論工作頻寬W和T模的截止波長λ再計算T模截止波長λ套用解方程的方法可以算出T波的截止波長λ、T模截止波長λ再求W實際上電磁波的截止狀態是一個漸變的過程。
經驗得出: 脊波導的有用工作頻寬W小於理論工作頻寬。換算成頻率範圍為:
Δf= f- f = 0. 98f- 1.18f
特性阻抗
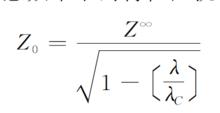一般表達式脊波導的特性阻抗是脊波導的重要參數之一 。它有不同的定義，有以電壓與功率之比定義的特性阻抗，有以電壓與電流之比定義的特性阻抗。在任意頻率下的特性阻抗的一般表達式為
式中Z 為頻率無限大時脊波導特性阻抗;λ為自由空間波長; λ為脊波導的截止波長。
功率容量
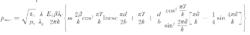脊波導理論最大功率容量:
式中 E為脊波導橫斷面脊的中心線上的電場強度; m= 1 為雙脊波導; m= 2 為單脊波導。選取的特性阻抗是電壓與功率比定義的 特性阻抗值偏大，即功率容量值偏小。
計算方法
從40年代起，Cohn開始研究脊波導的特性。Hofper和Pyle在Cohn的基礎上，分別用橫向諧振法和準靜態法對脊波導主模的截止波數作了計算，但對高次模卻無能為力。隨著人們認識到脊波導的寬頻特性在通信等領域的重要作用，隨後又有多種方法運用到脊波導的分析與求解。
有限元法是近似求解數理邊值問題的一種數值技術，廣泛套用於工程和數學問題。目前，二維問題的有限元方法已相當成熟，在電磁學和其他方面起著顯著的作用。有限元法可以分析任意形狀截面波導的特徵值問題。
