基本概念
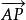羅氏平行直線
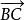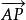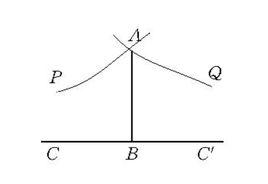
羅氏平行直線 羅氏平行直線 羅氏平行直線 羅氏平行直線 羅氏平行直線在羅氏平面上，若 ∥ ，則稱直線AP沿 方向(或 方向)平行於直線BC，記為AP∥BC於方向 (或 )。當方向一致時，直線間的平行具有對稱性和傳遞性。在羅氏平面上，過直線CC′外一點A，有且僅有兩條直線AP和AQ分別於不同的方向平行於CC′，在羅氏平面上，任何兩對平行線可以互相疊合，且二平行線在平行方向上無限接近，而在反方向無限遠離 。
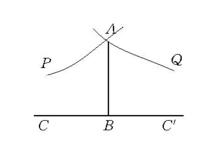圖1羅氏平行直線的基本性質
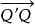羅氏平行直線 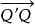羅氏平行直線 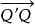羅氏平行直線定理1 (羅氏直線平行關係的對稱性定理) 若P'P //於方向，則Q'Q//P'P於同方向，即方向。
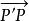羅氏平行直線定理2(羅氏直線平行關係的傳遞性定理) 對於不同的三條直線P'P，Q'Q和R'R，若P'P//Q'Q於方向，Q'Q//R'R於同方向，則P'P //R'R於同方向。
定理3 任何兩對平行直線可以互相疊合(即它們作為點的集合是契約的圖形)。
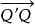羅氏平行直線定理4設P'P //Q'Q於方向，則在直線P'P上點M到直線Q'Q的距離，當M點沿平行方向移動是遞減，反之遞增。
雖然在中學數學課本中，關於羅氏平行直線的定義一點都沒有談及，但是卻簡單描述了羅氏平行直線的性質：兩條平行線，在一側無限接近，而在另一側無限遠離，非常直觀地描述了兩條平行直線的位置關係，易於學生理解，但羅氏平行直線的基本性質基本沒有提及，更談不上系統性地論述 。
