簡介
縱向放大率描述理想光具組的縱向共軛性質,在數學形式上是物象曲線的斜率。在近軸條件下所有光學元件均屬理想光具組。
物像曲線與共軛點的縱向放大率
物像曲線
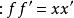 縱向放大率
縱向放大率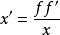 縱向放大率
縱向放大率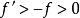 縱向放大率
縱向放大率按理想光具組理論,近軸共軛點的位置關係遵循牛頓公式 ,即 。像距x′與物距x的關係可用圖1所示的x′(x )曲線-物像曲線表示。圖中橫軸表示物空間,縱軸表示像空間 (縱軸正方向相當於像空間的從左向右方向)。不妨設 採用新笛卡兒符號法,並認為入射光線從左向右傳播。
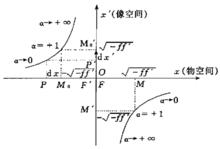 圖1.物象曲線x'(x)
圖1.物象曲線x'(x)這是位於第Ⅱ,Ⅳ象限的兩支反比例曲線,反映出共軛點位置的“交叉共軛”關係:F左側物體成像於F′右側;F右側物體成像於F′左側,且物離 F越遠,像離F′就越近。
共軛點的縱向放大率
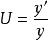 縱向放大率
縱向放大率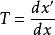 縱向放大率
縱向放大率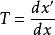 縱向放大率
縱向放大率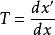 縱向放大率
縱向放大率按理想光具組理論,當物點P沿垂直於主光軸方向移動無限小距離y時,像點P′也在垂直於主光軸方向上移動某距離y′,橫向放大率 ,就表示像點P′相對於物點P移動的方向及距離,即表示共軛點P與P′的橫向共軛性質。類似地,若物點P平行於主光軸移動無限小距離dx,像點P′相應地移動dx′。可定義共軛點P與P′的縱向放大率 ,它反映在平行於主光軸的方向上,像點P′相對於物點P移動的方向及距離,即表征著共軛點P與 P′的縱向共軛性質。顯然, 就是物像曲線在P與P′處的斜率。在物、像移動的距離dx和dx′都很小的條件下,縱向放大率 是“點函式”,描述近軸共軛點P與P′的性質。
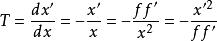 縱向放大率
縱向放大率由牛頓公式推得 ,把一些特殊的T值標在物像曲線相應位置上 (見圖1),便可清晰地觀察到如下規律:
1) 無論 P位於何處,總有T≥ 0(2條物像曲經均為上升曲線)。這表明物點P沿縱向移動時,其像點P′必沿相同方向移動:P點趨近F,像P′則沿同方向遠離 F′。
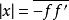 縱向放大率
縱向放大率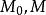 縱向放大率
縱向放大率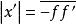 縱向放大率
縱向放大率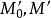 縱向放大率
縱向放大率2) 當|x|變小時,T變大。表明物點P趨近F,像P′沿同方向遠離F′時,像點P′相對於物點P移動的距離越來越大 .當 ( 處)且 ( 處),物、像移動的距離相等。
共軛線段的縱向放大率
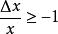 縱向放大率
縱向放大率圖2中,P移動有限距離Δx,有 ,即P始終在F的同一側移動到達P,則像P′移動Δx'到達P',且
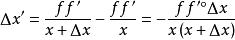 縱向放大率
縱向放大率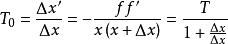 縱向放大率
縱向放大率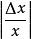 縱向放大率
縱向放大率令 ,T不僅與x有關,還與Δx有關,它不是“點函式” ,而反映端點為P ,P′,縱向長度為|Δx|和|Δx′|的一對共軛線段PP與 P′P′的關係,稱之為共軛線段的縱向放大率。由圖2知,當 Δx→0或 遠小於1時,T0→T,此時共軛線段的縱向放大率過渡到共軛點的縱向放大率。
 圖2.縱向線段的共軛關係
圖2.縱向線段的共軛關係由T的表達式及物像曲線的走勢,得出如下結論:
(1)恆有T≥ 0,與T≥0一樣,與物像曲線的上升性相聯繫;
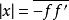 縱向放大率
縱向放大率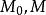 縱向放大率
縱向放大率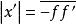 縱向放大率
縱向放大率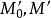 縱向放大率
縱向放大率(2)當Δx一定時,|x|越小,T就越大,這與T情況相似,但T= 1的位置未必是 ( 處)且 ( 處),而由 Δx 的值確定;
(3)當x一定時,T值就一定,但T卻隨Δx而變,且當x < 0時,Δx越大,T就越大;當x> 0時,Δx越大,T越小。
實際套用
縱向物體的成像規律
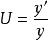 縱向放大率
縱向放大率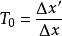 縱向放大率
縱向放大率縱向共軛性質與實際套用密切相關。若把前述y看作橫向物 (垂直於主光軸的線段)的長度,則y′就是橫向像的長度,而橫向放大率 就表示橫向物成像的性質(放大或縮小,正立或倒立)。如果把Δx看作縱向物 (平行於主光軸的線段)的長度,則Δx′就是縱向像的長度,縱向放大率 就表示縱向物成像的性質。|T|> 1,表示放大,|T|< 1,表示縮小。T> 0表示“正向”,T< 0表示“倒向” 。
由T的規律,得縱向物成像的特點:
(1)像相對於物恆屬“正向”,即箭頭成像指向不變 (T> 0);
(2)當某物靠近F時,其像從“縮小”逐漸過渡到“放大” ;
(3)端點P相同的縱向物,若長度不同,成像的性質就不同 (x 一定,T隨 Δx 而變 );
(4)成像不能保持幾何相似性 (圖2中,M位於物PP的中點,但M′卻不位於像P′P′的中點,物、像不相似 )。
照相機景深規律
景深,是指被攝物前後的一個縱深範圍。位於該範圍內的景物可在底片上形成可被辨認的像。對於焦距一定的相機,使光圈變小,可加大景深。當光圈一定時,景深還與T有關。
T越小,說明當P移動較大的距離|Δx,其像移動較小的距離|Δx′|,即P前後較大的範圍內景物都能在底片上形成可被辨認的像。也就是說,T越小,則景深越大。若Δx一定,|x|越大時,T越小,故景深越大。正因為如此 ,拍攝不太近的景物時,很遠的背景可以很清晰;拍攝近物時,稍遠的背景就變得模糊了。
在x處 (照相機總有x < f < 0),Δx越小,T也越小。設景物退後 (遠離相機 )和向前 (趨近相機 )移動相同的距離|Δx|,對應的縱向放大率 T <T ,物體背後的景深比前面的景深大,因而在拍攝景物時,較遠的背景可以很清晰,而稍前一點的景物就變得模糊。
