定義
經典組合學(classic combinaiorics)亦稱組合分析．組合學中的經典部分．它與許多數學分支在內容上有交又，目前還難以在一個統一的數學理論的範疇內進行表述和研究．大體上說，經典組合學是研究將某種離散對象按某個確定的約束條件進行安排的問題，一個符合確定的約束條件的安排稱為一個特定安排．
研究對象
經典組合學的研究對象可分為三大部分：
1．計數，包括生成函式(也稱母函式)、反演理論和有限差分計算．
2．序理論，包括有限偏序集和格，以及霍爾定理和拉姆齊定理等存在性定理．
3．布局，包括正交拉丁方、區組設計、正交表、阿達馬矩陣、差集等．
經典組合學常討論以下三個問題，即特定安排的存在性問題、特定安排的計數間題和尋求在某個最佳化準則下的最優解．
歷史起源
經典組合學也是數學的一個古老的分支．約在公元前2200年，中國就有所謂洛書河圖，即一種“用整數1，2，3，4，5，6，7，8，9，排成的3×3方陣，使得每行每列以及兩條對角線中的各數之和都是同一個數”的特定安排．傳說洛書是畫在神龜背上的，若用整數表出，則為著名的“農神”幻方：
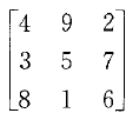河圖實質上是一個3階幻方在現代，組合的方法已在計算機科學、運輸、信息處理、工業計畫、電氣工程、試驗設計、抽樣、編碼、遺傳學、政治科學、考古學和其他領域被廣泛地套用，並取得了巨大的進展．
