簡介
adiabatic process
熱力學系統始終不與外界交換熱量 ， 即Q =0 的過程 。理想氣體準靜態絕熱過程的方程為pVr=常量，其中p 、V 是理想氣體的壓強、體積，γ=cP/cV是定壓熱容與定體熱容之比。根據熱力學第一定律，在絕熱過程中，系統對外所作的功等於內能的減少量。根據熱力學第二定律，在可逆的絕熱過程中，系統的熵不變。用良好絕熱材料隔絕的系統中進行的過程，或由於過程進行得太快，來不及與外界有顯著熱量交換的過程，都可近似地看作絕熱過程。例如內燃機、蒸汽機汽缸中工作物質的膨脹過程 ， 壓汽機汽缸中的壓縮過程，汽輪機噴管中的膨脹過程，以及氣象學中空氣團的升降過程，還有聲波在空氣中的傳播過程等，都可當作絕熱過程處理。
在和周圍環境之間沒有熱量交換或者沒有質量交換的情況下，一個系統的狀態的變化。大氣層中的許多重要現象都和絕熱變化有關。例如，在大氣層的下層通常存在著溫度隨高度而遞減，主要就是由於空氣絕熱混合的結果。導致水蒸汽凝結、雲和雨形成的降溫作用，主要是由於空氣上升時溫度下降的結果；晴朗的、乾燥的天氣通常是與空氣下沉引起的增溫變乾作用有關。上升空氣的降溫作用和下沉空氣的增溫作用主要是由於空氣的絕熱膨脹和絕熱壓縮的結果。如果一個受到增溫作用或降溫作用的系統通過輻射和傳導與周圍發生熱量交換，那么就稱之為非絕熱過程（diabaticprocess）。
絕熱過程是一個絕熱體系的變化過程，絕熱體系為和外界沒有熱量和粒子交換，但有其他形式的能量交換的體系，屬於封閉體系的一種。絕熱過程有絕熱壓縮和絕熱膨脹兩種。常見的一個絕熱過程的例子是絕熱火焰溫度，該溫度是指在假定火焰燃燒時沒有傳遞熱量給外界的情況下所可能達到的溫度。現實中，不存在真正意義上符合定義的絕熱過程，絕熱過程只是一種近似，所以有時也稱為絕熱近似。
絕熱過程分為可逆過程（熵增為零）和不可逆過程（熵增不為零）兩種。可逆的絕熱過程是等熵過程。等熵過程的對立面是等溫過程，在等溫過程中，最大限度的熱量被轉移到了外界，使得系統溫度恆定如常。由於在熱力學中，溫度與熵是一組共軛變數，等溫過程和等熵過程也可以視為“共軛”的一對過程。
如果一個熱力學系統的變化快到足以忽略與外界的熱交換的話，這一變化過程就可以視為絕熱過程，又稱“準靜態過程”。準靜態過程的熵增可以忽略，所以視作可逆過程，嚴格說來，在熱力學中，準靜態過程與可逆過程沒有嚴格區分，在某些文獻中被作為同義詞使用。
同樣的，如果一個熱力學系統的變化慢到足以靠與外界的熱交換來保持恆溫的話，該過程則可以視為等溫過程。
絕熱過程
用理想氣體狀態方程求解絕熱過程
Image:Adiabatic.svg
如圖所示，在絕熱膨脹過程（綠色粗線所示）中，氣體的內能因轉化為機械能做功（藍色部分）而減少對於經典氣體（非費米氣體、玻色氣體）的方程如下，是一個多方方程：
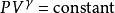絕熱過程（熱學）其中：
P表示壓強
V表示體積
ath> \gamma = \frac{C_{P}}{C<m_{V}} = \frac{\alpha + 1}{\alpha} </math>為多方指數。
<math> C _ P </math> 表示等壓比熱。
<math> C _ V </math> 表示等積比熱
<math> \alpha </math> 為總自由度除以2。對於單原子氣體（比如惰性氣體）而言，<math> \gamma = 5/3 </math>，對於雙原子氣體（如構成地球大氣主要成分的氮氣和氧氣）而言<math> \gamma = 7/5 </math>。
對於絕熱過程有：
<math> VT^\alpha = C </math>
C為常數，也可以寫作：
<math> TV^{\gamma - 1} = C </math>
連續系統的解法
因為絕熱過程沒有熱交換，所以<math>\delta Q=0 </math>，由熱力學第一定律，有
<math> \text{(1)} \qquad d U + \delta W = \delta Q = 0 </math>
dU為系統內能的變化量；δW是系統所做的功，做功必須耗費內能。由於δQ為零，可以得到
<math> \text{(2)} \qquad \delta W = P \, dV. </math>
理想氣體的內能可以由如下式子得到：
<math> \text{(3)} \qquad U = \alpha n R T </math>
R 為 理想氣體常數；n為系統的總分子數（因為絕熱過程無粒子交換，所以恆定不變）。
對（3）式兩邊微分，代入理想氣體狀態方程得到
<math> \text{(4)} \qquad d U = \alpha n R \, dT
= \alpha \, d (P V)
= \alpha (P \, dV + V \, dP). </math>
因為<math> C_{V} = \alpha R </math>，（4）式通常寫作 <math> d U = n C_{V} \, d T </math>
將（2）（3）（4）代入到（1），有：
<math> -P \, dV = \alpha P \, dV + \alpha V \, dP \,</math>
簡化得到：
<math> - (\alpha + 1) P \, dV = \alpha V \, dP \,</math>
兩邊同除以PV
<math> -(\alpha + 1) {d V \over V} = \alpha {d P \over P}. </math>
分別對P、V積分，得到
<math> \ln \left( {P \over P_0} \right)
= {-{\alpha + 1 \over \alpha}} \ln \left( {V \over V_0} \right). </math>
兩邊分別取冪：
<math> \left( {P \over P_0} \right)
= \left( {V \over V_0} \right)^{-{\alpha + 1 \over \alpha}}, </math>
消去負號：
<math> \left( {P \over P_0} \right)
= \left( {V_0 \over V} \right)^{\alpha + 1 \over \alpha}. </math>
因此得到：
<math> \left( {P \over P_0} \right) \left( {V \over V_0} \right)^{\alpha+1 \over \alpha} = 1
</math>
和
<math> P V^{\alpha+1 \over \alpha} = P_0 V_0^{\alpha+1 \over \alpha} = P V^\gamma = Const </math>
Const為常數。
[編輯]離散系統的解法
從狀態1到狀態2，系統的內能變化為：
<math> \text{(1)} \qquad \delta U = \alpha R n_2T_2 - \alpha R n_1T_1 = \alpha R (n_2T_2 - n_1T_1) </math>
同時，氣體做功為：
<math> \text{(2)} \qquad \delta W = P_2V_2 - P_1V_1 </math>
因為絕熱，所以有：
<math> \text{(3)} \qquad \delta U + \delta W = 0 </math>
將（1）（2）式分別帶入得到：
<math> \alpha R (n_2T_2 - n_1T_1) + (P_2V_2 - P_1V_1) = 0 \qquad \qquad \qquad </math>
或：
<math> \frac {(P_2V_2 - P_1V_1)} {-(n_2T_2 - n_1T_1)} = \alpha R \qquad \qquad \qquad </math>
因為實際情形下，通常可以假定氣體質量數不變，該式可以簡化為：
<math> \frac {(P_2V_2 - P_1V_1)} {-(T_2 - T_1)} = \alpha n R \qquad \qquad \qquad </math>
等熵線圖
Image:Entropyandtemp.PNG
等熵與等溫線圖，紅線為等溫過程，黑線為等熵過程。等熵線又稱絕熱線，是指P-V圖中等熵的一條曲線，如右圖黑色線條所示。
等熵線有以下性質：
像等溫線一樣對稱的趨近V軸與P軸。
每條等熵線只穿過一次等溫線。
等熵線與等溫線相似，但斜率更大。
若等溫線凹向45度方向處，則等熵線凹向31度方向處。
P-V圖上一系列的等溫—等熵線所繪出的眼形方塊顯示出向原點方向移動的趨勢。參見能斯特定理。
