連續系統
定理內容
連續系統的拉普拉斯變換對應的終值定理如下所示:
設有連續函式f(t),當t趨於無窮時,f(t)的極限存在,且有:
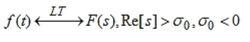 終值定理
終值定理則終值定理可表達為:
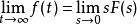 終值定理
終值定理該定理說明了,當滿足一定使用條件時,可由S域的象函式直接得到時域連續函式的終值。
注意:終值定理是取 的極限,因而s=0的點應在sF(s)的收斂域內,否則不能套用終值定理。
證明
由微分定理,有
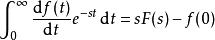 終值定理
終值定理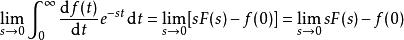 終值定理
終值定理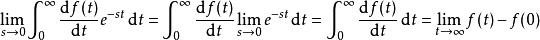 終值定理
終值定理令 ,對等式兩邊取極限,得 等式左邊為 於是有
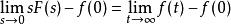 終值定理
終值定理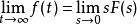 終值定理
終值定理即 。
典例
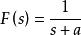 終值定理
終值定理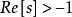 終值定理
終值定理如函式f(t)的象函式 , 。
求原函式f(t)的初值和終值。
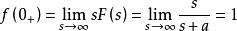 終值定理
終值定理解:(1)由初值定理,得: ;
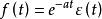 終值定理
終值定理由F(s)的原函式 ,顯然以上結果對a>0或a<0都是正確的。
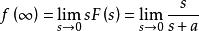 終值定理
終值定理(2)由終值定理,得: ,
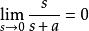 終值定理
終值定理① 若a>0,則有 ;
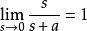 終值定理
終值定理② 若a=0,則有 ;
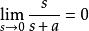 終值定理
終值定理③若a<0,則有 ;
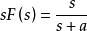 終值定理
終值定理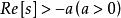 終值定理
終值定理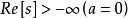 終值定理
終值定理對於a≥0, 的收斂域分別為 ,和 ,顯然 s=0在收斂域內,因而結果 ①②正確;對於a<0,sF(s)的收斂域為Re[s]>-a=|a|,s=0不在收斂域內, 因而結果③不正確,由F(s)的原函式容易驗證以上的結果。
離散系統
定理內容
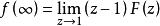 終值定理
終值定理離散系統的z變換對應的終值定理如下所示:
終值定理適用於右邊序列,用於由象函式直接求得序列的終值,而不必求得原序列。
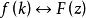 終值定理
終值定理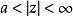 終值定理
終值定理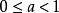 終值定理
終值定理如果序列在k<M時f(k)=0,設: , ,且 ,
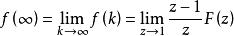 終值定理
終值定理則序列的終值 :
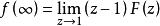 終值定理
終值定理或寫為:
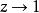 終值定理
終值定理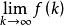 終值定理
終值定理上式中是取 的極限,因此最終終值定理要求z=1在收斂域內(即0≤a<1),這時 存在。
典例
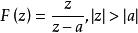 終值定理
終值定理某因果序列的z變換為(設a為實數): ,
求 。
解:
(1)利用初值定理可得
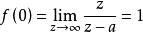 終值定理
終值定理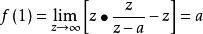 終值定理
終值定理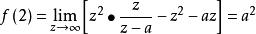 終值定理
終值定理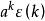 終值定理
終值定理上述象函式的原序列為 ,可見以上結果對任意實數a均正確。
(2)利用終值定理可得
① 當|a|<1時
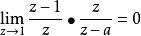 終值定理
終值定理,
z=1在F(z)的收斂域內,終值定理成立,因而有:
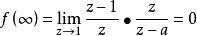 終值定理
終值定理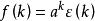 終值定理
終值定理不難驗證,原序列 ,故|a|<1時以上結果正確。
② 當|a|=1時
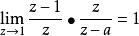 終值定理
終值定理若a=1,則有 ,此時原序列 ,結果正確。
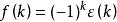 終值定理
終值定理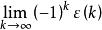 終值定理
終值定理若a=-1,則有 ,此時原序列 ,這時 不收 斂,因而終值定理不成立。
③ 當|a|>1時,z=1不在收斂域內,終值定理也不成立。
難點和建議
難點:現有的多數教材與參考書均直接給出了定理的使用條件和證明過程的敘述方式,並未解釋為何使用定理時需要條件的限定,而且在證明過程中,往往迴避了連續信號中含有衝激函式項的情況。這樣的處理方式割裂了定理使用條件和定理內容之間的聯繫,使讀者在學習過程中感到十分困惑。
建議:首先從定理的使用條件出發,分析特定象函式的拉普拉斯逆變換; 其次尋找定理使用條件與定理本身之間的關聯;最後再給出定理的嚴格證明,即先從頻域到時域進行引導,再從時域到頻域證明 。
注意事項
終值定理的使用條件是當t趨於無窮時,連續函式f(t)的極限存在,或者說s=0在sF(s)的收斂域內,需結合收斂域的知識 。
需理解系統函式和極零點分析相關知識。
已知f(t)為因果函式,則有:
(1)當收斂域包含S域虛軸時,s=0在sF(s)的收斂域內,滿足終值定理使用條件;
(2)當收斂域剛好在虛軸上時,只有階躍函式ε(t)的終值存在;
(3)當收斂域不包含虛軸時,時域函式一般為發散函式,終值肯定不存在,也就無法使用終值定理。
(4)終值定理的使用條件和初值定理不同,只要終值存在,即收斂域滿足使用條件即可。當F(s)為假分數時,同樣可以使用定理 。
1.終值定理的使用條件是當t趨於無窮時,連續函式f(t)的極限存在,或者說s=0在sF(s)的收斂域內,需結合收斂域的知識 。
2.需理解系統函式和極零點分析相關知識。
3.已知f(t)為因果函式,則有:
(1)當收斂域包含S域虛軸時,s=0在sF(s)的收斂域內,滿足終值定理使用條件;
(2)當收斂域剛好在虛軸上時,只有階躍函式ε(t)的終值存在;
(3)當收斂域不包含虛軸時,時域函式一般為發散函式,終值肯定不存在,也就無法使用終值定理。
(4)終值定理的使用條件和初值定理不同,只要終值存在,即收斂域滿足使用條件即可。當F(s)為假分數時,同樣可以使用定理 。
其它套用
可用於計算自控原理中的穩態誤差 。
使用時應注意:必須明確終值定理的套用條件,f(t)的拉氏變換F(s)在s右半平面及虛軸上解析,即沒有極點,計算時首先應該判斷系統的穩定性。