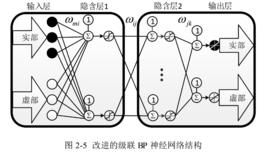
多級網路條件
多年來,人們提出了大量的模式識別方法,這些方法各有優點,但也不可避免地存在一定的局限性和適用條件.為了把各種方法有機地結合起來,取長補短,提高系統的整體性能,人們提出了多級神經網路的結構模型.多級神經網路結構的每一級子系統,通常都由特徵提取模組和神經網路模組所組成.特徵提取模組從輸入數據中提取特徵矢量,基於該特徵矢量,神經網路模組在學習階段對所有訓練數據進行學習,而在工作階段則對輸入到本級的數據進行分類判別,包括識別輸出和拒識輸出兩種情況.不妨假定:某一級的特徵提取模組所提取的特徵能有效地代表一部分輸入樣本的本質特徵,因此這一部分樣本在該級中將成功地得到識別,其餘的樣本則由於特徵不清而被拒識,送入到下一級進行基於另外一種特徵提取和神經網路結構的分類判別。
一個好的多級神經網路結構應滿足兩個條件:
(1)有效設計每一級的特徵提取模組,儘可能使每一級的特徵提取方法相互獨立,互為補充;
(2)合理設計各級神經網路模組,使得該神經網路能有效地拒識那些在該級特徵下模糊不清的樣本,從而使誤識率儘可能降低.多級神經網路結構的整體性能在很大程度上依賴於每一級子系統誤識率的高低,而前幾級的誤識率尤其關鍵。
網路介紹
一般的神經網路是固定好拓撲結構,然後訓練權重和閾值。級聯相關神經網路是從一個小網路開始,自動訓練和添加隱含單元,最終形成一個多層的結構。
級聯神經網路(Cascaded Neural Network,以下簡稱 CNN),該模型由神經網路組成瀑布結構。所有變數在輸入 CNN 之前都要被預處理程式標準化為[0,1]之間,同時,需通過最大相關性最小冗餘(Maximum Relevance Minimum Redundancy,以下簡稱 MRMR)法則的篩選。
結構模型
其結構模型如右圖所示:
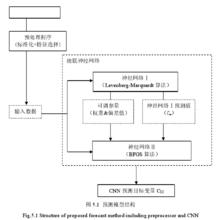 級聯神經網路
級聯神經網路CNN 由神經網路Ⅰ和神經網路Ⅱ組成,兩個神經網路分別有不同的學習算法來預測,但具有相同的多層感知器結構(Multi-Layer Perceptron,以下簡稱 MLP),MLP 有足夠數量的隱藏神經元,以至於能夠在期望的精度下近似任何連續的多元函式。此外,根據 Kolmogorov 定理,MLP 有適當數量的神經元能夠使用一個隱藏層解決問題,因此,本模型中的兩個神經網路的 MLP 都具有一個隱藏層。
神經網路Ⅰ會傳輸兩種結果值到神經網路Ⅱ,一種是經過神經網路Ⅰ訓練獲得地可調參量,包括權重和偏差值,前文提到,兩個神經網路具有相同的 MLP,因此,神經網路Ⅰ獲得的權重和偏差值可以直接傳輸給神經網路Ⅱ,從而使神經網路Ⅱ的輸出目標變數更加準確;另一種是神經網路Ⅰ預測的目標變數。神經網路Ⅰ向神經網路Ⅱ傳輸結果值,神經網路Ⅰ的訓練會終止,此時,神經網路Ⅱ開始學習進程,以此來取代以往模型中神經網路Ⅱ隨機開始。除了神經網路Ⅰ的結果值,一組隨機的可調參數初始值也將進入到神經網路Ⅱ的學習進程中,從而保證神經網路Ⅱ獲得更加全面的信息。
算法
適合的學習算法的選取將使 CNN 比單個神經網路更加全面,將獲得更適合的可調參量。Catala 研究得出,Levenberg Marquardt(以下簡稱 LM)法和 Broyden Fletcher Goldfarb Shanno (以下簡稱 BFGS)法是基於牛頓法演變出的兩個最有效的用於預測的神經網路訓練算法。
BFGS算法
Broyden Fletcher Goldfarb Shanno 算法 BFGS 算法同樣是由最佳化中的牛頓法演變而來,N. Amjady 認為 BFGS 算法是準牛頓法中最成功的神經網路算法。準牛頓法中,二階導數的海森矩陣函式將被最小化,不用再對其做其他計算,而是通過分析連續梯度向量來更新海森矩陣。在 BFGS 算法中,以下步驟從初始的猜測值 x0和近似海森矩陣 B0開始重複,直到 x 收斂。
BFGS 算法從一個合適的初始值開始,能夠進行更好的解空間收索,神經網路的解空間可以看成一個向量,它的維度是神經網路的可調參量。
LM算法
LM 算法是一個快速的學習算法,在訓練初期,LM 算法得 MLP能夠快速地學習問題,同時,它的訓練誤差會快速下降。
交叉驗證
(Cross-validation)
為了避免神經網路產生過擬合,在 CNN中採取交叉驗證,交叉驗證又被稱作循環估計,是一種統計學上將數據樣本切割成較小子集的實用方法。運用交叉驗證把 CNN 的一部訓練集區分出來,當作驗證集,而用剩餘的訓練集來對CNN 中各神經網路進行測試訓練,此時,驗證集對於各神經網路來說是未知的。各神經網路訓練的預測誤差對於驗證集來說是一個衡量其月度預測誤差的標準,神經網路的泛化能力,所謂泛化能力(generalization ability)是指機器學習算法對新鮮樣本的適應能力。學習的目的是學到隱含在數據對背後的規律,對具有同一規律的學習集以外的數據,經過訓練的網路也能給出合適的輸出,也能得到評估。訓練和驗證的結果越相似,則說明交叉驗證的效果越好。各神經網路訓練階段的每一步進程都受驗證誤差(驗證誤差為驗證集的誤差)的限制,當各神經網路在訓練時開始出現過擬合,驗證誤差也會開始上漲,當驗證誤差上漲到一定限值時,訓練將提前終止,從而很準確地防止了過擬合現象的產生。
性能
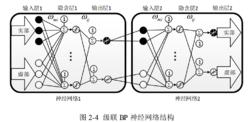 級聯神經網路
級聯神經網路通過兩個結構不同的神經網路進行級聯,可以大大增加網路性能,但這樣也會大大加大網路的複雜度,可以從圖看出,不管在什麼位置增加一個神經元,其資源複雜程度都是倍數增長的,然而在測試中發現,複雜程度的增加在性能的改善上面並不是直接線性關係的,故將網路進行簡化,由於神經網路的核心為隱含層和其權值向量,故保留隱含層,將第一層的輸出層與第二層的輸入層合併,這樣可以把雙層結構的神經網路複雜度簡化為單層的複雜度,通過這樣的簡化,可以在保證核心隱含層不變的情況下,去掉很大一部分網路結構。
套用
由於級聯相關神經網路具有以下優點:學習速度快;自己決定神經元個數和深度;訓練集變化之後還能保持原有的結構;不需要後向傳播錯誤信號。級聯神經網路可套用於人工成本預測研究、人臉檢測方法的研究、年降雨量預測等諸多領域,在電力管理、軍事、醫療、智慧型製造等多個行業也得到了重要套用。