數學模型
要求一部分或全部決策變數必須取整數值的規劃問題稱為整數規劃(integer programming,簡記IP)。不考慮整數條件,由余下的目標函式和約束條件構成的規劃問題稱為該整數規劃問題的松馳問題( slack problem )。若松馳問題是一個線性規劃,則稱該整數規劃為整數線性規劃(integer linearprogramming)。
整數線性規劃數學模型的一般形式為:
 純整數線性規劃
純整數線性規劃 純整數線性規劃
純整數線性規劃分類
整數線性規劃問題可以分為下列幾種類型:
(1)純整數線性規劃(Pure integer linear programming):指全部決策變數都必須取整數值的整數線性規劃。有時,也稱為全整數規劃。
(2)混合整數線性規劃(Mimed integer linear programming):指決策變數中有一部分必須取整數值,另一部分可以不取整數值的整數線性規劃。
(3)0-1型整數線性規劃((Zero-one integer linear programming):指決策變數只能了取值0或1的整數線性規劃。
特點
松馳問題作為一個線性規劃問題,其可行解的集合是一個凸集,任意兩個可行解的凸組合仍為可行解。整數規劃問題的可行解是它松馳問題可行解集合的一個子集,任意兩個可行解的凸組合不一定滿足整數約束條件,因而不一定仍為可行解。由於整數規劃問題的可行解一定也是它的松馳問題的可行解(反之則不一定),所以,前者最優解的目標函式值不會優於後者最優解的目標函式值,即鬆弛問題的最優解是整數規劃問題最優解的上限。
在一般情況下,松馳問題的最優解不會剛好滿足變數的整數約束條件,因而不是整數規劃的可行解,自然就不是整數規劃的最優解。此時,若對松馳問題的這個最優解中不符合整數要求的分量簡單地取整,所得到的解不一定是整數規劃問題的最優解,甚至也不一定是整數規劃問題的可行解。
求整方法
典型的求整數規劃的方法有割平面法、分支定界法、完全枚舉法、以及適用於指派問題的匈牙利解法等。
(1)完全枚舉法:對於可行域有界的整數線性規劃問題,整 數線性規劃的可行解是一個有限集,將 這個集內的每一個點對應的目標函式值 都一一計算出來,然後從中找出最優者 ,則為整數線性規劃的最優解。適於變數個數不大於10的0-1型整數線性規劃。
(2)分支定界法:分支定界解法是一種部分枚舉法,通過不斷地 分割鬆弛問題的可行域並進行比較,最終求得整數線性規劃問題的最優解。它的解題思路是先求解整數線性規劃的鬆弛問題,如果其最優解不符合整數條件,則用增加約束的辦法求出整數線性規劃問題的上下界,並把鬆弛問題的可行域分成互不重疊的子區域,再求解這些子區域的鬆弛問題,不斷縮小整數線性規劃問題上下界的差距,最後取得整數線性規劃問題的最優解。
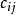 純整數線性規劃
純整數線性規劃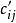 純整數線性規劃
純整數線性規劃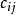 純整數線性規劃
純整數線性規劃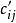 純整數線性規劃
純整數線性規劃(3)匈牙利解法的思路為:1)若從指派問題的係數矩陣()的某行(或某列)各元素分別減去一個常數k,得到一個新的矩陣(),為()和()為係數矩陣的兩個指派問題有相同的最優解。2)獨立0元素:位於不同行不同列的0元素。3)若在係數矩陣中找到n個獨立0元素,則對應的指派方案總費用(或時間、成本等) 為零,即為原指派問題的最優解。
(4)割平面法:割平面法是R. E. Gomory於1958年提出的一種方法,它主要用於求解純整數規劃。若伴隨規劃的最優解不滿足整數約束,則有兩條途徑可走:
1)將整數規劃問題分解成幾個子規劃,只要不斷查清子問題的解的情況,原問題也因此得到解決。(即分枝定界法)
2)不斷切割原問題伴隨規劃的可行域,使它在不斷縮小的過程 中,將原問題的整數最優解逐漸暴露,且趨於可行域極點的位置。(即割平面法)

