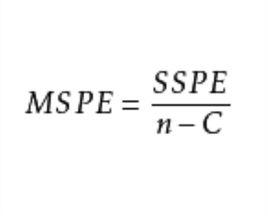基本介紹
在重複試驗的回歸模型中,設自變數的取值水平共C個,共試驗n次,其中每個水平F重複獨立試驗n次(∑n=n)。設因變數在第i水平下的第j次觀察值為Y,i=1,…,C,j=1,…,n,令
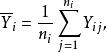 純均方誤差
純均方誤差表示第i水平下因變數的平均數,則
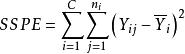 純均方誤差
純均方誤差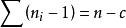 純均方誤差
純均方誤差稱為 純誤差平方和,其自由度為,SSPE是模型失擬的檢驗中所使用的量。將誤差平方和除以自由度即為 純均方誤差,通常用 MSPE表示,即
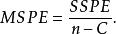 純均方誤差
純均方誤差定理
 純均方誤差
純均方誤差 純均方誤差
純均方誤差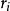 純均方誤差
純均方誤差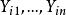 純均方誤差
純均方誤差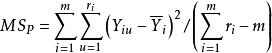 純均方誤差
純均方誤差 純均方誤差
純均方誤差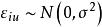 純均方誤差
純均方誤差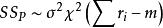 純均方誤差
純均方誤差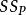 純均方誤差
純均方誤差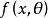 純均方誤差
純均方誤差設有m個試驗點,在每一個處有次重複,其試驗結果為,令,則MS是的一個無偏估計。當相互獨立時,。且的分布不依賴於的選擇 。
證明 從略。
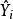 純均方誤差
純均方誤差 純均方誤差
純均方誤差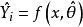 純均方誤差
純均方誤差 純均方誤差
純均方誤差令表示模型在點外的擬合值(),則在點外的殘差為
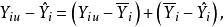 純均方誤差
純均方誤差從而有
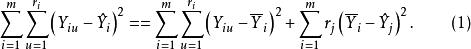 純均方誤差
純均方誤差即
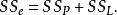 純均方誤差
純均方誤差其中SS為殘差平方和,SS為純誤差平方和,SS為擬合誤差平方和。並且對應於(1)有如下的自由度分解:
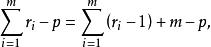 純均方誤差
純均方誤差其中p為模型未知參數的個數。顯然,m≥p。如果m=p,則模型無擬合誤差,即數據完全擬合模型。從(1)可知,模型的殘差平方和由兩部分構成。一部分是 純誤差平方和,另一部分是擬合不佳所引起的 誤差平方和。
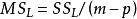 純均方誤差
純均方誤差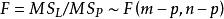 純均方誤差
純均方誤差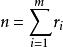 純均方誤差
純均方誤差令,則,這裡。由此,可以用於檢驗模型擬合的好壞 。
相關知識
失擬檢驗是一種用來判斷回歸模型是否可以接受的檢驗。判斷模型好壞主要通過殘差分析,而殘差是由兩部分組成的;一部分是隨機的,即使模型擬合得再好,它也消除不了,稱為隨機誤差或純誤差;另一部分與模型有關,模型合適,這部分的值就小,模型不合適,這部分的值就大,稱為失擬誤差。失擬檢驗就是以失擬誤差對純誤差的相對大小來作判斷的: 倘失擬誤差顯著地大於純誤差,那么就放棄模型;如並不顯著地大於純誤差,那么就可以接受該模型。失擬檢驗的前提是要求在自變數x的若干值處進行重複試驗,設在x處有n次重複試驗 (j=1,2,…,c),記
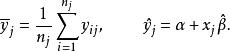 純均方誤差
純均方誤差則有
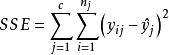 純均方誤差
純均方誤差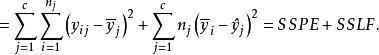 純均方誤差
純均方誤差其中: SSE—殘差平方和,SSPE—純誤差平方和,SSLF—失擬的平方和(擬合誤差平方和)。SSE,SSPE,SSLF的自由度分別為n-p-1,n-c,c-p-1。在獨立、正態及等方差假定之下
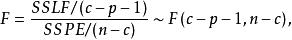 純均方誤差
純均方誤差對於給定置信度水平 (1-α),如果F<F(c-p-1,n-c)就認為失擬是不顯著的,就接受該模型;如果F>F(c-p-1,n-c),則認為失擬不顯著,因而模型可以拒絕。儘管失擬檢驗原則上能夠檢驗任何種類的回歸模型,但通常用它來檢驗模型的線性假設是否合理 。