簡介
CSPs將其問題中的單元(entities)表示成在變數上有限條件的一組同質(homogeneous)的集合, 這類問題透過"約束補償方法"來解決。CSPs是人工智慧和運籌學 的熱門主題,因為它們公式中的規律，提供了共同基礎來分析、解決很多看似不相關的問題。 CSPs通常呈現高複雜性, 需要同時透過啟發式搜尋和聯合搜尋 的方法，來在合理的時間內解決問題。 布爾可滿足性問題 (SAT), 可滿足性的理論 (SMT)和回答集程式設計 (ASP) 可以算是某種程度上的約束滿足問題。
定義
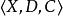約束滿足問題正式來說，約束滿足問題定義為一個三元組 ，其中
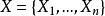約束滿足問題是變數的集合,
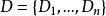約束滿足問題是各個變數的定義域集合,而
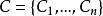約束滿足問題是限制條件的集合。
約束滿足問題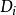
約束滿足問題
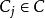約束滿足問題
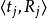約束滿足問題
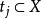約束滿足問題
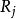約束滿足問題 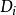約束滿足問題
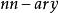約束滿足問題每個變數 可以在非空的定義域 中取出。每個限制條件(Constraint) 依序對應一對 ，其中 是 {\displaystyle n} n-tuple的變數， 則是在定義域中，其對應到的子集合上得到的維的關係。 變數的評估(evaluation)是一個函式，其從變數的子集合映射到一組特定的集合，集合內為定義域的子集合所對應到的值，也就是
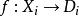約束滿足問題
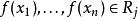約束滿足問題
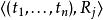約束滿足問題如果，則此評估(evaluation) f滿足條件限制。
如果一個評估不違反任何的條件限制，我們說這個評估是無矛盾的(consistent)。 如果一個評估包含了所有的變數，我們說這個評估是完備的(complete)。 如果一個評估無矛盾而且完備的，我們說這個評估是一個解(solution)，這樣的評估就會用來解決CSP。
CSPs的解決方法
定義域有限的約束滿足問題通常利用搜尋方法來解決。最常用的技術是回溯法(backtracking)、約束傳遞constraint propagation，以及局部搜尋local search的改良。
回溯法 是一種遞歸算法，它保持部分變數的賦值。一開始，所有的變數都還沒被賦值。在每一個步驟中，先選取一個變數，並且將所有可能的值依次賦予該變數。對於每一個值，在限制條件下的局部賦值的無矛盾性(consistency)都進行檢查。在匹配無矛盾(consistency)的情況下，就會遞歸地往下調用。當所有的值都試過，算法則回溯上層。在這個基本回溯算法中，無矛盾性(consistency)被定義為滿足所有的條件限制，且這些條件限制的變數已被賦值。若干回溯變數存在。 回溯法 提高了檢查無矛盾性的效率。 回跳法 可以使在某些在某些情況中，透過回溯”一個以上的變數“，來省去部分的搜尋。 約束學習則藉由減少新的條件限制,來避免部分的搜尋。 可預見性也常常在回溯法中套用，用來去預期選擇一個變數或值的影響，因此常常用來預先判定一個子問題什麼時候滿足或不滿足。 約束傳遞 (Constraint propagation)技術是用來修飾一個CSP的方法。更精確地說，是一種方法，用來增強一種形式的局部一致性，是一種條件牽連到一組變數或條件限制的一致性。約束傳播套用在各個領域。一來,它把問題轉化為一個等價但通常是最簡單的解決方法。 二來，他可以用來驗證滿足或不滿足於問題。 一般來說他不保證會發生，但是它總是會發生一些形式的約束傳遞(Constraint propagation)或某些種類的問題。 最有名的慣用的局部一致性是 弧協調性，超弧一致性，和路徑一致性。 最流行的方法是AC-3約束傳播算法，該算法可以運行弧的一致性。
局部搜尋方法 是不完全滿足的算法。人們可能找到解決問題的方法， 但這方法可能令我們失望。其反覆更改變數來改進整個任務，而得以運作。在每一步，要更改少量變數的值,與整體目標數量的增加條件限制以滿足的任務。 最小衝突算法是局部搜尋算法和基於特定CSPs原則。在實踐中,局部搜尋似乎工作當這些變化也受隨機選擇。集成搜尋和局部搜尋被開發了,導致混合算法。
CSPs的理論方面
判定問題
CSPs也研究計算複雜性問題和有限模型理論. 一個重要的問題是，是否為每一組的關係、套都可視為CSPs選自只使用關係設定不是在p 或 NP-完全問題. 如果這樣一個二分法真實可靠， 那么CSPs提供已知的最大的一個NP 子集,避免NP-intermediate 問題，其存在是證明了Ladner's 理論 在這種假定下 P ≠ NP. Schaefer's 二分法理論 處理所用變數相關時的情況布爾數學運算符, 也就是， 對一個定義域大小為2的。 最近的一個促進dichotomoy二分定理推廣到一個更大的類的事務。
功能問題
相同的情形存在於功能類別之間，FP 和 #P.通過一般的Ladner's 理論, FP 和 #P-complete 也存在問題如果 FP ≠ #P。在這種決策下， 一個#CSP問題被定義為一組關係。每個問題需要輸入布爾 公式作為輸入，任務是計算數字令人滿意的工作。這可以進一步推廣利用大域大小和附上一個權重，對每一個滿意的賦值和計算這些權值的總和。 眾所周知任何複雜的#CSP權重問題既不是FP 也不是 #P-hard問題。
CSPs的變型
動態CSPs
動態CSPs (DCSPs) 是有用的，當原有的問題形式以某種方式改變，通常是由於約束集進化，因為要考慮環境。DCSPs被當做一系列的靜態CSPs ，每一個都是轉變的前一個變數和約束可以添加或刪除限制(放鬆)。信息在初始的配方發現問題可以用來提煉下一個。解決的方法可分為根據信息的方法在轉讓:
•Oracles: 解決之前發現的序列CSPs作為啟發式方法指導解決當前CSP從零開始。
•Local repair: 每個CSP計算從解決部分問題之前的修復與Local search。局部搜尋不約束。
•Constraint recording: 新的約束是定義在每一階段的搜尋代表學習群決策不一致。在這些約束進行了新的CSP問題。
靈活的CSPs
經典的CSPs處理約束很嚴格，意味著強制的 (每一解決方案必須滿足所有問題) 並且刻板的 (意味著,以至於他們必須被完全滿足,否則他們是完全違反了)。 靈活的 CSPs 放寬假設, 部分的放寬限制對不遵循的的也一樣解決問題。 這類似於preference-based planning. 一些類型的靈活 CSPs 包括:
•MAX-CSP， 在那裡有好些約束允許受侵犯的質量,並通過測量方法多少滿意的約束。
•加權 CSP，使每一個MAX-CSP違反約束加權根據預定義的偏好。因此,更重要的是滿足約束的優先考慮。
•CSP模糊的約束關係，在這種情況下約束滿足是變數的連續函式，從完全滿足到完全不滿足。
