基本介紹
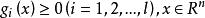 起作用約束
起作用約束 起作用約束
起作用約束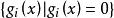 起作用約束
起作用約束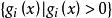 起作用約束
起作用約束考慮非線性規劃問題,假設不等式約束,,具有一階連續導數。問題的可行域為,對於某些下標,點x的鄰域限制了可行點的範圍,即沿著某些方向稍微離開x點都將導致違背這些約束,這樣的約束稱為在點x處 起作用約束。反之,對於約束,當點稍微離開x時,無論什麼方向都不會違反約束,稱為在點x處 不 起作用約束。
相關分析
對於一般的約束最佳化問題,其約束包含兩類:
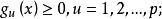 起作用約束
起作用約束不等式約束 (1a)
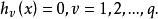 起作用約束
起作用約束等式約束 (1b)
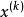 起作用約束
起作用約束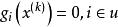 起作用約束
起作用約束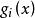 起作用約束
起作用約束在可行設計點處,對於不等式約束,如果有,則稱第i個約束為
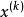 起作用約束
起作用約束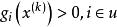 起作用約束
起作用約束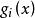 起作用約束
起作用約束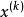 起作用約束
起作用約束可行點的 起作用約束;否則,有,則稱為可行點的 不起作用約束。顯見,只有在可行域 D邊界上的點才有起作用約束,而且是該點所在邊界約束自身;而所有各約束對可行域內部的設計點都是不起作用的約束。
對於式(1b)的等式約束,凡是滿足該約束的任一可行點,該等式約束都是起作用約束。
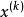 起作用約束
起作用約束由於約束最佳化問題的最優解不僅與目標函式有關,而與約束集合的性質也有關。在可行設計點處,起作用約束在該點鄰域不僅起到限制可行域範圍的作用,而且還可提供有關可行搜尋方向的信息。又由於約束最優點x*,一般是發生在起作用約束上,則不起作用約束對求最優點的問題,就認為不產生任何影響,所以可看作是略去不起作用約束;而把注意力集中到設計點的起作用約束上,而把全部起作用約束當作等式約束問題求最優點處理 。
約束條件
在最佳化設計中,目標函式取決於設計變數,而設計變數的取值範圍都有各種限制條件。每個限制條件都可寫成包含設計變數的函式,稱為 約束條件或設計約束。因為它是設計變數的函式,也稱為 約束函式。
約束函式可用等式或不等式描述。如果約束函式能夠反映設計變數之間明顯的函式關係,稱為 顯式約束;否則,稱為 隱式約束。
等式約束是對設計變數的嚴格約束,起著降低設計自由度的作用,其形式為:
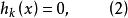 起作用約束
起作用約束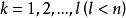 起作用約束
起作用約束式中,,l為等式約束的數目,n為設計維數。
不等式約束,其形式為:
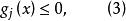 起作用約束
起作用約束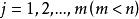 起作用約束
起作用約束式中,,m為不等式約束的數目。
根據約束的性質,分為 幾何約束(邊界約束)和 性能約束。
幾何約束:根據某種設計要求,設計變數必須滿足的某些幾何條件以及只對設計變數的取值範圍加以限制的那些約束。
性能約束:指滿足特定工作性能而建立的約束條件。
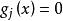 起作用約束
起作用約束對於等式約束而言,設計變數所代表的沒計點必須在式(2)所表示的面(或線)上,稱為 起作用約束或 緊約束。對於不等式約束,極限情況所表示的幾何面或線將設計空間分成兩部分:一部分中所有設計均滿足所有的約束條件,這部分空問稱為設計點的可行域;另一部分所有點均不滿足約束條件,稱為設計點的不可行域。在可行域內的設計點,稱為可行設計點,可行域也是可行設計點的集合。位於可行域邊界上的設計點亦是可行點,過該點的約束為起作用約束,否則為不起作用約束;非可行域是不滿足約束條件設計點的集合。
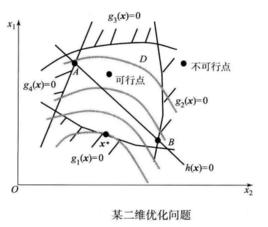
如圖1所示的某二維最佳化設計問題,包含四個不等式約束和一個等式約束。圖中,分別表示了可行域、不可行域、可行點、不可行點、起作用約束和不起作用約束 。
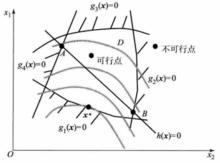 圖1(a)某二維最佳化問題
圖1(a)某二維最佳化問題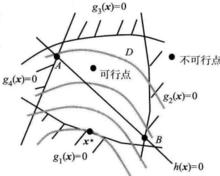 圖1(b)
圖1(b)