簡介
Mealy machine的名字來自這個概念的提出者,在1951年寫了A Method for Synthesizing Sequential Circuits的狀態機的先驅G. H. Mealy。
運作機制
Mealy機提供了密碼機的一個根本的數學模型。例如考慮拉丁字母表的輸入和輸出,一個Mealy機可以被設計用來把給定字母的字元串(一序列輸入)處理成密碼字元串(一序列輸出)。但是,儘管你可能使用Mealy模型來描述恩尼格瑪密碼機,狀態圖對於提供設計複雜密碼機的靈活方式而言太複雜了。
Mealy狀態機與Moore有限狀態機不同,Mealy有限狀態機的輸出不單與當前狀態有關,而且與輸入信號的當前值有關。Mealy有限狀態機的輸出直接受輸入信號的當前值影響,而輸入信號可能在一個時鐘周期內任意時刻變化,這使得Mealy有限狀態機對輸入的回響發生在當前時鐘周期,比Moore有限狀態機對輸入信號的回響要早一個周期。因此,輸入信號的噪聲可能影響在輸出的信號。
形式定義
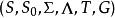 米利型有限狀態機
米利型有限狀態機Mealy機是6-元組,構成自:
 米利型有限狀態機
米利型有限狀態機狀態的有限集合
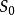 米利型有限狀態機
米利型有限狀態機 米利型有限狀態機
米利型有限狀態機開始狀態(也叫做初始狀態) ,它是 的元素
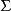 米利型有限狀態機
米利型有限狀態機叫做輸入字母表的有限集合
 米利型有限狀態機
米利型有限狀態機叫做輸出字母表的有限集合
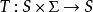 米利型有限狀態機
米利型有限狀態機轉移函式
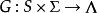 米利型有限狀態機
米利型有限狀態機輸出函式
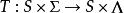 米利型有限狀態機
米利型有限狀態機在某些公式中,轉換和輸出函式合併為單個函式 。
Mealy機和摩爾機的比較
1.Mealy機器的規定往往較少:
弧(n2)而不是狀態(n)的不同輸出。
2.摩爾機器使用更安全:
輸出在時鐘邊沿變化(總是在一個周期後)。
在Mealy機器中,輸入更改可能會在邏輯完成後立即導致輸出更改 - 當兩台機器互連時出現大問題 - 如果不小心,可能會發生異步反饋。
3.Mealy機器對輸入的反應更快:
在相同的周期內反應 - 不需要等待時鐘。
在Moore機器中,可能需要更多邏輯來將狀態解碼為輸出 - 在時鐘邊沿之後更多的門延遲。
並非所有時序電路都可以使用Mealy模型實現。 一些時序電路只能作為摩爾機器實現。
圖
Mealy機器的狀態圖將輸出值與每個轉換邊緣相關聯(與Moore機器的狀態圖相反,Moore機器將輸出值與每個狀態相關聯)。
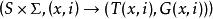 米利型有限狀態機
米利型有限狀態機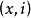 米利型有限狀態機
米利型有限狀態機當輸入和輸出字母表都是Σ時,還可以將Mealy Automata與Helix有向圖相關聯。該圖具有狀態和字母對的頂點,每個節點都是一度的,而 的後繼是自動機的下一個狀態和自動機輸出時的字母x和 它讀取字母i。 如果自動機是雙向的,則該圖是不相交周期的並集。
樣例
簡單的
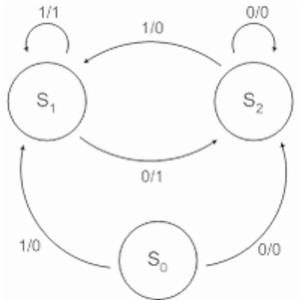
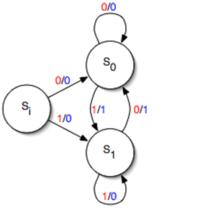 Mealy機圖
Mealy機圖一台簡單的Mealy機器有一個輸入和一個輸出。每個過渡邊緣都標有輸入值(以紅色顯示)和輸出值(以藍色顯示)。機器以Si狀態啟動。(在此示例中,輸出是兩個最新輸入值的異或;因此,機器實現邊緣檢測器,每次輸入翻轉時輸出一個,否則輸出零。)
複雜的
更複雜的Mealy機器可以有多個輸入和多個輸出。
套用
Mealy機器為密碼機提供了基本的數學模型。例如,考慮到拉丁字母表的輸入和輸出字母表,可以設計一個Mealy機器,給定一串字母(一系列輸入)可以將其處理成加密的字元串(一系列輸出)。然而,儘管可以使用Mealy模型來描述Enigma,但狀態圖太複雜,無法提供設計複雜加密機器的可行方法。
Moore / Mealy機器,也是時鐘任意滴答輸出的DFA。現代CPU,計算機,手機,數字時鐘和基本電子設備/機器都有某種有限狀態機來控制它。
簡單的軟體系統,特別是可以使用正則表達式表示的系統,可以建模為有限狀態機。有許多這樣的簡單系統,例如自動售貨機或基本電子設備。
通過找到兩個有限狀態機的交集,可以以非常簡單的方式設計例如交換訊息的並發系統。例如,交通信號燈是由多個子系統組成的系統,例如同時工作的不同交通信號燈。
一些套用示例:
•數字分類
•看著計時器
•售貨機
•紅綠燈
•掃碼機
•氣泵