定義
同期形成,同一成因,具有一定相關產狀的所有節理稱節理組。例如受同一地應力的作用形成的區域性分布基本同一產狀的平行節理;在沉積岩里一組通常平行於傾向和另一組平行於走向的節理;在塊狀岩漿岩和變質岩中三組不同產狀的節理。
研究意義
岩體的性質有岩石和結構面兩方面共同決定,在地下工程的施工中,造成岩體破壞加重的主要原因來源於結構面的脆弱,所以,研究岩體的強度、變形和運動等,就要從研究岩體的結構面著重入手,結構面的存在,使得岩體呈現出不連續性、不均勻性、強烈各向異性等特性,也造成了岩體的力學性能在強度和穩定性方面比完整岩體的力學性能大幅度的降低,因此,大量工程中岩體的失穩和破壞都是以岩體內部的結構面為突破口,像裂隙、節理的發育和擴展等,從而出現大的變形,產生大的位移,造成了岩土工程的破壞。
岩土工程中,由於施工的進行,會造成岩體中地應力的釋放、調整和重分布,使得岩體的一些部位產生應力集中現象,會使在岩體中某些薄弱的地帶節理裂隙增長和擴展,產生新的破裂面,以及一些新的裂隙,已有破壞面的不斷擴展、貫通,最後導致整個岩體的破壞。由此可以看出,岩體中存在的產狀不同節理和裂隙對岩土工程的影響很大,研究這些岩體中節理和裂隙在工程施工過程中的起裂、擴展、貫通過程,對於研究岩體的特性、揭示岩體的破壞機理、分析岩土工程的穩定性具有重要意義。 因此,我們在認識了節理形成的破壞機制、產生條件等規律後,便可以利用節理面的組合形式、展布特徵、最大組數等規律進一步研究岩體的強度與穩定性。
節理面測量方法
常用的節理面測量方法有掃描線法(Sean Line Surveys)和取樣窗法(Sampling Windowu Svreyrs):掃描線法是用一條或幾條測線,平行或任意角度斜交展布在節理露頭面上,記錄與測線相交那些節理面的參數;取樣窗法是在一定範圍內的有效露頭面上填圖,記錄每條節理的參數和每條節理的相對位置,一般被測定的參數有節理的產狀、間距、跡長、節理面的起伏度、張開度和節理中的充填物等。
節理統計方法
傳統的節理統計方法有節理極密圖法、傾向(走向)玫瑰花圖法、頻率直方圖法、等角度統計方法等。
極密圖法
極點密度圖處理過程大致經歷三個步驟:
作節理極點密度圖,作輪廓線圈定各組節理的極點;
從原始數據中,將屬於各組節理的數據分別挑選出來;
統計各組節理的節理性質指標,確定其分布及數字特徵。
1.作節理極點密度圖,作輪廓線圈定各組節理的極點;
2.從原始數據中,將屬於各組節理的數據分別挑選出來;
3.統計各組節理的節理性質指標,確定其分布及數字特徵。
頻率直方圖法
對全部節理進行傾向數據的頻率統計,繪製直方圖,在極點投影網上確定極點比較集中的傾向扇形區及其範圍。
對各傾向扇內的節理進行傾角數數據的頻率統計,繪製直方圖,在極點投影網上確定極點集中的傾角環及其範圍。一般,通過以上兩過程即可確定出一些扇狀環形極密區及其範圍。
屬於各扇狀環形極密區內的節理,可能屬於不同傾向的節理組,對其再次進行傾向數據的頻率統計,以此分開各節理組的數據,從而確定各組節理的扇狀環形極密區確切的變化範圍。至此,全部節理即被各個扇形環狀極密區分為若干組。
1.對全部節理進行傾向數據的頻率統計,繪製直方圖,在極點投影網上確定極點比較集中的傾向扇形區及其範圍。
2.對各傾向扇內的節理進行傾角數數據的頻率統計,繪製直方圖,在極點投影網上確定極點集中的傾角環及其範圍。一般,通過以上兩過程即可確定出一些扇狀環形極密區及其範圍。
3.屬於各扇狀環形極密區內的節理,可能屬於不同傾向的節理組,對其再次進行傾向數據的頻率統計,以此分開各節理組的數據,從而確定各組節理的扇狀環形極密區確切的變化範圍。至此,全部節理即被各個扇形環狀極密區分為若干組。
最大距離法
最大距離法的基本原則是使分組後的節理組間距離最大,而組內距離最小。
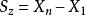 節理組
節理組以節理傾向為例,設有n個節理,按其傾向從0°-360°排列。以X表示節理傾向,X表示第i個節理的傾向。用{i,… j}表示由第i個節理至第j個節理終止的節理組,其中1≤ i≤ j≤ n。組間距離以S=(X-X)表示,即組間距離為相鄰兩組中前一組最小值與後一組最大值之差。組內距離用組內極差d=X-X表示,n個節理傾向總極差為一常數。
設n個節理被分為k組,以X和X分別表示第k組節理中第1個和最後一個節理的傾向。
則組內距離差和為
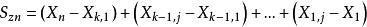 節理組
節理組組間距離和為
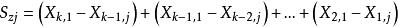 節理組
節理組則
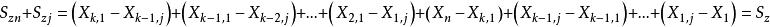 節理組
節理組因此當S最大時,S最小。由於組間距離為相鄰節理傾向之差,如果把n-1個(X-X)按從大到小排列,把n個節理分成k組只需找前k-1個(X-X)所對應的X作為分組點即可。
節理統計方法有許多,但在實際操作中,人為因素影響較大,特別是當前普遍使用的極密圖法和玫瑰花圖法。使用極密圖處理傾角時,10°以內的誤差很難識別出來;而使用玫瑰花圖法時,分組數及間隔大小具有很強的人為確定因素,難免存在系統誤差。相比之下,最大距離法具有理論的科學性和實際套用的可行性、有效性,具有較大的套用價值。

