簡介
等溫結晶（isothermal crystallization）
溫度恆定時的結晶。它是研究和展示高聚物結晶行為常用的實驗方法之一。等溫結晶過程可用與結晶程度相關的物理量。如比容隨時間的變化（等溫結晶曲線）來描述。比容可用膨脹計法測量。測量時先將試樣加熱到熔點以上保持適當的時間，然後快速降溫到等溫結晶選定的溫度，保持溫度不變．考察比容隨時間的變化。等溫結晶的初期可有一個比容不變的結晶誘導期，然後比容變小，表明發生結晶變化。比容變化的速度逐漸增大，然後減小，比容值趨向恆定，表明結晶過程的終了。從等溫結晶曲線可獲得該溫度下結晶速率和結晶程度以及與結晶成核、生長有關的信息。高聚物等溫結晶曲線的數據可用Avrami方程並處理。
等溫結晶轉變
金屬玻璃的結晶過程是一種在固態中發生的相反應或相轉變過程。我們可以用固態相轉變理論來研究它。為了方便起見，假設這種相轉變理論是在等溫條件下來進行論述的，但是，實際情況常常是在變溫情況下（即不等溫條件下）發生相轉變的。不同的金屬玻璃在結晶過程中的轉變機理也不儘是相同的。目前所研究的金屬玻璃的結晶過程大部分是符合Johnson-Mehl-Avrami方程的，有少數幾種金屬玻璃的結晶過程不符合J-M-A方程，而符合“自動催化”反應方程或其他反應方程（如像Kissinger反應方程）。這裡先介紹由J-M-A方程表達的相轉變分數X（體積比）與等溫退火時間t的關係。
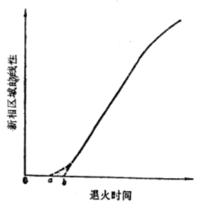新相區域的等溫生長示意圖假設固態發生的相轉變過程是一個包含有新相成核和長大的過程。設原相為α，新相為β。在相轉變過程中，要經過一定的時間新相才開始長大，這段時間稱為孕育時間t。這就是說，當t<t時，無新相體積，只有在t=t之後，新相才開始長大。右圖示出了新相區域的等溫生長示意圖。從此圖中可以看出，新相區域的線性尺寸與時間t的關係中有一段是線性關係。在這段時間內，生長速率u是恆定的，不隨時間而變。將圖的線性部分延長，與橫軸t交於b，Ob所表示的時間稱為孕育時間。它是計算新相體積長大時，用恒生長速率μ計算的起始時間，也可把0a表示的時間作為孕育時間，但這時，起始的生長速率就不是恆定不變的，而是隨時間而增加的，當t很大時，生長速率降低，這從圖中便可看出。這種情況的發生是由於新相核相互之間的碰撞所引起的，因為碰撞嚴重地影響了新相的生長。但有些相變系統，其孕育時間接近於零，這就表明在轉變開始之前，新相β的相核早已存在於系統之中。
Johnson，Mehl和Avrami；首先提出關於固態中發生的相轉變分數X與時間t的關係的計算方法。在他們的處理中，不僅考慮了未轉變的餅相區域的成核，而且也考慮到已轉變區域的成核。後者稱為“幻想核”。在計算新相體積時，不扣除“幻想核”數所得的體積稱為“擴張體積"。他們計算了實際轉變體積與侶擴張體積靜之間的關係，進而得到了在等溫相變過程中，轉變分數X（體積比）與時間t的關係式。假設新相的成核邃率I和生長速率μ不隨時間t變化。對子三維生長系統，轉變分數X與時間t的關係式如下：
X=1-exp（（-π/3）Iμ t ）
等溫結晶及阿弗拉米關係
不同結構的高聚物其結晶速度的差別是很大的，例如聚乙烯在熔融後，即使將其投入液氮中也不能得到無定形的聚合物。而聚對苯二甲酸乙二酯則不同，只要將其熔體投入室溫的水中，它即會因驟冷而呈透明狀，說明它的結晶速度很慢。人們研究結晶速度的目的，在於了解聚合物的結構和外界條件對結晶速度和結晶形態的影響，進而通過結晶過程去控制結晶度和結晶形態，從而進一步達到控制產品性能的目的。
實驗研究結晶速度有兩種方法：一是在一定溫度下觀察結晶度隨時間的變化，即所謂等溫結晶曲線的方法；另一種方法是直接在附有溫控裝置的顯微鏡下觀察球晶大小隨時間的變化。
等溫結晶曲線
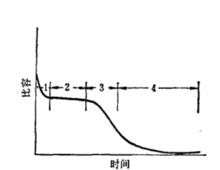圖4-25 結晶過程中比容的變化圖聚合物在結晶過程中隨著分子重排會發生體積收縮，觀察體積收縮值即可跟蹤結晶過程。一般是用體積膨脹計（以下簡稱體膨計）進行。首先將試樣放入體膨計內，在熔點以上的某溫度下使聚合物熔融適當時間，然後在指定的結晶溫度下觀察毛細管內水銀面的下降。開始由於冷卻而引起急劇的收縮，見圖4-25（區域1），隨之進入水平部分——誘導期（區域2），然後才開始結晶（區域3）。結晶開始時速度很快，以後逐漸減慢（區域4），最後達到視平衡，要達到真正的平衡，有時要長期等待。典型等溫結晶曲線的全貌呈倒S型，如圖4-25所示。
利用差示掃描量熱計(DSC)測量在結晶過程中的熱效應亦能很好地研究聚合物的等溫結晶，此法用樣量少，同時可進行快速結晶的測量，這是體膨計法無法測量的。利用DSC法所得的典型等溫曲線如圖4-26所示。
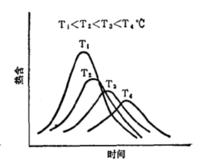圖4—26 差示掃描量熱法測得的等溫結晶線直接觀察的方法是使用附有加熱裝置的“熱台偏光顯微鏡”。將試樣置第一熱台下以指定的溫度加熱熔融，然後迅速切換至第二熱台（即為指定結晶溫度），在恆溫下觀察球晶半徑隨時間的變化。這種方法的優點是直觀，便於研究其生長過程。
阿弗拉米關係式
不同結晶性的高聚物的等溫結晶曲線都具有倒S的形狀，不同溫度的等溫線是一組S形曲線。如何從此了解結晶的過程?人們對金屬和低分子物質的結晶的研究已相當成熟，曾總結出阿弗拉米關係式，而摩根（Morgan）和曼德爾克恩（Mandelkern）等人發現可將它用於聚合物體系。
高聚物熔體結晶時一般呈球晶，這些球晶在各個方向以等速生長，隨著時問的進展，最終鄰近球晶相互間會發生衝突，在兩個球晶衝突處，晶體的生長遂即停止（相碰以後的結晶過程則叫二次結晶）。很顯然，主要應該考慮的是還沒有發生衝突以前的結晶情況。同時體系中核的形成是不受限制的，這些核在三度空間半徑方向上以等速G向外長大，在dx時問內結晶的重量為dW，在時間x秒的球晶的半徑應為Gx，故整個球晶的重量即為：4/3π（Gx） ρ。
式中ρ——球晶的比重。
開始熔體是均相的，未預先加入任何晶核，這時核產生的速度為N個/cm ·s，熔體比重為ρ，起始熔體的總重為W，則在dx時間內，在全部熔體內產生的核的數目為：N（W/ρ）dx
從熔體中結晶的量為：
dW=N（W/ρ）dx·4/3π（Gx）ρ
對於圓板狀結晶體和纖維狀晶體亦可同樣地進行計算，所得結果形式相同，一般以下式表示：
ln（1-W/W）=-kt
或以下式表示：
W/W=1一exp（-kt）
這就是阿弗拉米關係式。式中k——結晶速率常數；n——阿弗拉米指數。
聚合物的等溫結晶
差示掃描量熱法（DSC）是測量聚合物等溫結晶的一種快速而靈敏的方法。試樣需先行熱處理，消除熱歷史的影響，然後快速冷卻到結晶溫度，隨時間測量放熱。
許多變數，如結晶溫度、添加劑（如染料）的成核性質、分子量分布和加入共聚單體均會影響聚合物的結晶性質，影響其外觀、尺寸穩定性和熔程等項性能。
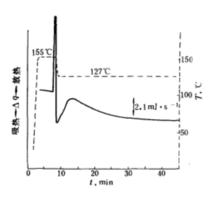聚乙烯在127℃的等溫結晶等溫結晶的實驗條件與所測聚合物試樣密切相關，無法規定統一的條件。茲以聚乙烯為俐，可採用如下實驗條件：
試樣量 10mg
量程 0.8236mJ·s ·cm
時間基數 0.7874min·cm
起始溫度 室溫
退火溫度和時間 155℃，保持10min
結晶溫度 127℃
氣流 N，流速 50ml·min
按上述條件測得的聚乙烯等溫結晶DSC曲線如圖。
採用DSC可測定聚合物等溫結晶的熱效應，並可由DSC曲線的結晶放熱峰進行結晶速率等的解析。
上圖是用精工SSC/560S測定的PET從265℃急劇冷卻到205℃的等溫結晶DSC曲線。速冷DSC曲線隨之達到新的基線，而後呈結晶放熱峰，結晶終止再度恢復到基線。
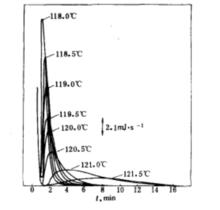HDPE在不同溫度結晶的DSC曲線右圖是HDPE在不同溫度結晶的DSC曲線，結晶速率隨結晶溫度而異，溫度在118.0～121.5℃之間，隨溫度降低結晶速率加快，結晶終止時間縮短。另外，從實驗結果可見：當溫度改變0.5℃時結晶速率已有明顯改變，這就要求十分精確地控制恆定溫度；在所試的溫度範圍，數分鐘即完成結晶過程，因此體系必須熱惰性小，能迅達到設定的恆溫狀態。
