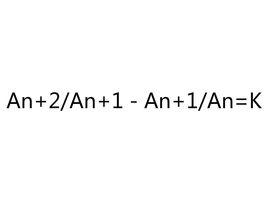定義
若數列滿足a/a-a/a=k,則稱該數列為等比差數列,其中k為公比差。
如1,2,8,48,384,……就是一組以1為首項,2為第二項,2為公比差的等比差數列。
性質
已知等比差數列的前2項以及公比差,其通項公式求解步驟如下:
①令b=a/a,b=a/a,則{b}是等差數列,由公式可求出{b}通項公式。
②可得a/a=b的公式,利用疊乘相消法a/a×a/a×……×a/a=b×b×……×b可求得a/a的公式,等式兩邊同乘a即可得到{a}的通項公式。
如:求a=1,a=2,k=2的等比差數列的通項公式。
令b=a/a,b=a/a,則{b}是以2為首項,2為公差的等差數列,可求得b=2n。
則a/a=b=2n,利用疊乘相消法a/a×a/a×……×a/a=b×b×……×b可求得a/a=2×4×6×……×2(n-1)=(n-1)!×2 ,等式兩邊同乘a即可得到a=(n-1)!×2 。
套用
等比差數列常出現在用不完全歸納法推斷一串數的未知項,即找數字規律時。其在解題方面的套用較少。
另一定義
關於等比差數列的定義說法不一,有人認為,其概念應為:一個首項為a,以後各項由遞推式a=qa+d(其中q和d為常數,k≥2)確定的數列,稱為“等比差數列”。(當d=0時為等比數列,當q=1時為等差數列)。
這時等比差數列的通項公式與前n項和的公式為:
a=aq +(1-q )/(1-q)·d
S={(1-q )[a-d/(1-q)]+nd}/(1-q)
兩個定義的爭議點在於,等比差數列是前後兩項之差為等比數列,還是前後兩項之比為等差數列。兩種定義可導出兩種性質不同的數列,都值得研究。