第二基本定理

第二基本定理是亞純函式奈望林納理論中重要定理。奈望林納在亞純函式的研究中建立了兩個基本定理。他這方面的工作使值分布理論出現了新面貌，並開始了值分布的近代理論，即奈望林納理論。

定義

第二基本定理是亞純函式奈望林納理論中重要定理。

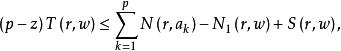第二基本定理

設w(z)為亞純函式，a(k=1,2,...,p)是p(>2)個互異的複數（有窮或無窮），則有第二基本定理如下： 其中N(r,w)是重值點數目函式，S(r,w)為餘項，滿足S(r,w)=O(logrT(r,w))(r→∞)。

提出者背景

奈望林納早期在亞純函式方面有重要貢獻。

1922年，他在解析函式的邊界性質方面證明了：若f(Z)∈N，f(Z)不恆等於0，則f(Z)幾乎處處有非切向邊界值f(eiQ)，且log|f(eiQ)|∈L'[0,2π]。

1925年，他在亞純函式的研究中建立了兩個基本定理。他這方面的工作使值分布理論出現了新面貌，並開始了值分布的近代理論，即奈望林納理論。

奈望林納理論

奈望林納理論即近代純函式值分布理論，是由芬蘭數學家奈望林納(Nevanlinna,R.)於20世紀20年代創立的。他還建立了兩個基本定理且引入新的概念，使得已有的理論或呈現嶄新的面貌，或得到重要的推廣。

亞純函式奈望林納理論還被推廣於代數體函式、亞純曲線和多復變亞純映射等方面，並且成為研究復域常微分方程解析理論的有力工具。