第一極大值原理

第一極大值原理（first maximum principle）是描述位勢局部極大值蘊涵整體極大值的一個原理。

簡介

第一極大值原理是描述位勢局部極大值蘊涵整體極大值的一個原理。

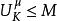第一極大值原理

若對任何μ≥0， 在μ的支集supp μ上成立蘊涵該不等式在整個Ω成立，則稱K滿足第一極大值原理。

性質

α核當0<α≤2時滿足該原理，而當2<α<n時不滿足該原理。

推廣

廣義極大值原理是第一極大值原理的推廣。

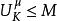第一極大值原理

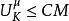第一極大值原理

若存在常數C≥0，對任何μ≥0，使 在suppμ上成立蘊涵 在整個Ω成立，則稱K滿足廣義極大值原理。

α核都滿足廣義極大值原理。

位勢

一般位勢是經典位勢的一種直接推廣形式，常為一個二元數值函式（核）關於某個測度的積分。

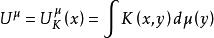第一極大值原理

設(Ω,)是一個可測空間，K(x,y)是從Ω×Ω到[-∞,+∞]的可測函式，μ是上的實測度。若對每個x∈Ω，下式中的積分有意義，則由Ω到[-∞,+∞]的函式 稱為μ以K為核的一般位勢，簡稱位勢。