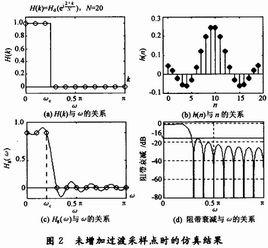
基本定義
為了減少頻譜能量泄漏，可採用不同的截取函式對信號進行截斷，截斷函式稱為窗函式，簡稱為窗。
誤差。
泄漏與窗函式頻譜的兩側旁瓣有關，如果兩側瓣的高度趨於零，而使能量相對集中在主瓣，就可以較為接近於真實的頻譜，為此，在時間域中可採用不同的窗函式來截斷信號。
數位訊號處理的主要數學工具是傅立葉變換．而傅立葉變換是研究整個時間域和頻率域的關係。不過，當運用計算機實現工程測試信號處理時，不可能對無限長的信號進行測量和運算，而是取其有限的時間片段進行分析。做法是從信號中截取一個時間片段，然後用截取的信號時間片段進行周期延拓處理，得到虛擬的無限長的信號，然後就可以對信號進行傅立葉變換、相關分析等數學處理。無限長的信號被截斷以後，其頻譜發生了畸變，原來集中在f(0)處的能量被分散到兩個較寬的頻帶中去了（這種現象稱之為頻譜能量泄漏）。為了減少頻譜能量泄漏，可採用不同的截取函式對信號進行截斷，截斷函式稱為窗函式，簡稱為窗。
相關原理
不同的窗函式對信號頻譜的影響是不一樣的，這主要是因為不同的窗函式，產生泄漏的大小不一樣，頻率分辨能力也不一樣。信號的截斷產生了能量泄漏，而用FFT算法計算頻譜又產生了柵欄效應，從原理上講這兩種誤差都是不能消除的，但是我們可以通過選擇不同的窗函式對它們的影響進行抑制。(矩形窗主瓣窄，旁瓣大，頻率識別精度最高，幅值識別精度最低；布萊克曼窗主瓣寬，旁瓣小，頻率識別精度最低，但幅值識別精度最高)。
濾波器設計
設計濾波器時，通常給定的幅度特性是分段恆定的、且在頻帶的邊界有不連續點。逼近這樣的特性，需用無限衝激回響(IIR)數字濾波器。為採用有限衝激回響(FIR)實現，可以選合適的、有限時寬窗序列對無限衝激回響序列加權，以構成有限衝激回響數字濾波器實現給定特性。因為時間域內兩個序列相乘，頻率域內等效為兩個序列離散傅立葉變換的卷積。因此，窗函式與給定濾波特性的卷積可達到以有限衝激回響逼近給定特性的目的。
用經典法周期圖作功率譜估計時，為了提高解析度而要求增加記錄數據的長度，但其結果會導致周期圖的波動增大，亦即估計方差的增大。為了平滑這類譜估計，並減小估計方差，可對數據進行加窗，然後再作周期圖估計，以達到減小方差和提高解析度的折衷。
相關原理
不同的窗函式對信號頻譜的影響是不一樣的，這主要是因為不同的窗函式，產生泄漏的大小不一樣，頻率分辨能力也不一樣。信號的截斷產生了能量泄漏，而用FFT算法計算頻譜又產生了柵欄效應，從原理上講這兩種誤差都是不能消除的，但是我們可以通過選擇不同的窗函式對它們的影響進行抑制。(矩形窗主瓣窄，旁瓣大，頻率識別精度最高，幅值識別精度最低；布萊克曼窗主瓣寬，旁瓣小，頻率識別精度最低，但幅值識別精度最高)
窗函式選擇
對於窗函式的選擇，應考慮被分析信號的性質與處理要求。如果僅要求精確讀出主瓣頻率，而不考慮幅值精度，則可選用主瓣寬度比較窄而便於分辨的矩形窗，例如測量物體的自振頻率等；如果分析窄帶信號，且有較強的干擾噪聲，則應選用旁瓣幅度小的窗函式，如漢寧窗、三角窗等；對於隨時間按指數衰減的函式，可採用指數窗來提高信噪比，下面簡要介紹各種窗函式的優缺點。
矩形窗屬於時間變數的零次冪窗。矩形窗使用最多，習慣上不加窗就是使信號通過了矩形窗。這種窗的優點是主瓣比較集中，缺點是旁瓣較高，並有負旁瓣，導致變換中帶進了高頻干擾和泄漏，甚至出現負譜現象。
三角窗亦稱費傑（Fejer）窗，是冪窗的一次方形式。與矩形窗比較，主瓣寬約等於矩形窗的兩倍，但旁瓣小，而且無負旁瓣。
漢寧窗又稱升餘弦窗，漢寧窗可以看作是3個矩形時間窗的頻譜之和，或者說是 3個 sinc（t）型函式之和，而括弧中的兩項相對於第一個譜窗向左、右各移動了 π/T，從而使旁瓣互相抵消，消去高頻干擾和漏能。可以看出，漢寧窗主瓣加寬並降低，旁瓣則顯著減小，從減小泄漏觀點出發，漢寧窗優於矩形窗．但漢寧窗主瓣加寬，相當於分析頻寬加寬，頻率分辨力下降。
海明窗也是餘弦窗的一種，又稱改進的升餘弦窗。海明窗與漢寧窗都是餘弦窗，只是加權係數不同。海明窗加權的係數能使旁瓣達到更小。分析表明，海明窗的第一旁瓣衰減為一42dB．海明窗的頻譜也是由3個矩形時窗的頻譜合成，但其旁瓣衰減速度為20dB/（10oct），這比漢寧窗衰減速度慢。海明窗與漢寧窗都是很有用的窗函式。
高斯窗是一種指數窗。高斯窗譜無負的旁瓣，第一旁瓣衰減達一55dB。高斯富譜的主瓣較寬，故而頻率分辨力低．高斯窗函式常被用來截短一些非周期信號，如指數衰減信號等。
常用函式
矩形窗
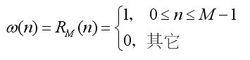矩形窗函式矩形窗屬於時間變數的零次冪窗。矩形窗使用最多，習慣上不加窗就是使信號通過了矩形窗。這種窗的優點是主瓣比較集中，缺點是旁瓣較高，並有負旁瓣，導致變換中帶進了高頻干擾和泄漏，甚至出現負譜現象。
三角窗
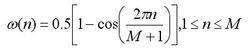漢寧(Hanning)窗三角窗亦稱費傑（Fejer）窗，是冪窗的一次方形式。與矩形窗比較，主瓣寬約等於矩形窗的兩倍，但旁瓣小，而且無負旁瓣。
漢寧窗
哈明(Hamming)窗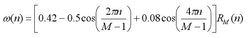
布萊克曼(Blackman)窗漢寧窗又稱升餘弦窗，漢寧窗可以看作是3個矩形時間窗的頻譜之和，或者說是 3個 sinc（t）型函式之和，而括弧中的兩項相對於第一個譜窗向左、右各移動了 π/T，從而使旁瓣互相抵消，消去高頻干擾和漏能。可以看出，漢寧窗主瓣加寬並降低，旁瓣則顯著減小，從減小泄漏觀點出發，漢寧窗優於矩形窗．但漢寧窗主瓣加寬，相當於分析頻寬加寬，頻率分辨力下降。
海明窗
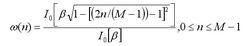凱澤(Kaiser)窗海明窗也是餘弦窗的一種，又稱改進的升餘弦窗。海明窗與漢寧窗都是餘弦窗，只是加權係數不同。海明窗加權的係數能使旁瓣達到更小。分析表明，海明窗的第一旁瓣衰減為一42dB．海明窗的頻譜也是由3個矩形時窗的頻譜合成，但其旁瓣衰減速度為20dB/（10oct），這比漢寧窗衰減速度慢。海明窗與漢寧窗都是很有用的窗函式。
高斯窗
高斯窗是一種指數窗。高斯窗譜無負的旁瓣，第一旁瓣衰減達一55dB。高斯富譜的主瓣較寬，故而頻率分辨力低．高斯窗函式常被用來截短一些非周期信號，如指數衰減信號等。
主要類型
實際套用的窗函式，可分為以下主要類型：
a) 冪窗--採用時間變數某種冪次的函式，如矩形、三角形、梯形或其它時間（t）的高次冪；
b)三角函式窗--套用三角函式，即正弦或餘弦函式等組合成複合函式，例如漢寧窗、海明窗等；
c)指數窗--採用指數時間函式，如 形式，例如高斯窗等。
