簡介
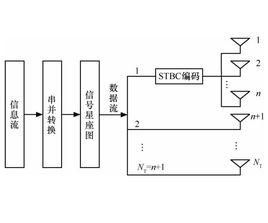
直到20世紀90年代早期,大多數關於無線通信的工作都集中在無線鏈路的一端 - 通常是在接收器處。Gerard J. Foschini和Michael J. Gans,Foschini和Emre Telatar的研究論文擴大了無線通信可能性的範圍,表明對於高度散射的環境,當天線陣列是用於連結的兩端。利用多個天線的替代方法依賴於具有多個發射天線並且僅可選地具有多個接收天線。由Vahid Tarokh,Nambi Seshadri和Robert Calderbank提出,這些空時編碼(STC)比單天線系統實現了顯著的錯誤率改進。他們最初的方案是基於格子碼,但Siavash Alamouti和後來的Vahid Tarokh,Hamid Jafarkhani和Robert Calderbank利用更簡單的區塊代碼來開發時空分組碼(STBC)。 STC涉及傳輸多個冗餘數據副本以補償衰落和熱噪聲,希望它們中的一些可能以比其他狀態更好的狀態到達接收器。特別是在STBC的情況下,要傳送的數據流以塊的形式編碼,這些塊在間隔的天線之間並且跨時間分布。雖然必須具有多個發射天線,但是沒有必要具有多個接收天線,儘管這樣做可以提高性能。這種接收不同數據副本的過程稱為多樣性接收,在Foschini 1998年的論文之前,這一過程主要得到了研究。
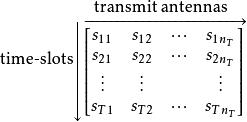
STBC通常由矩陣表示。每行代表一個時隙,每列代表一個天線隨時間的傳輸。
 空時分組碼
空時分組碼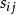 空時分組碼
空時分組碼 空時分組碼
空時分組碼 空時分組碼
空時分組碼 空時分組碼
空時分組碼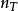 空時分組碼
空時分組碼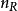 空時分組碼
空時分組碼 空時分組碼
空時分組碼這裡,是要在天線的時隙中傳送的調製符號。有時隙和發射天線以及接收天線。該塊通常被認為是'length'
 空時分組碼
空時分組碼STBC的碼率測量它在一個塊的過程中平均每個時隙傳輸的符號數。如果一個塊編碼個符號,則碼率為
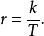 空時分組碼
空時分組碼只有一個標準STBC可以實現全速率(速率1)-Alamouti的代碼。
正交
最初引入的STBC和通常研究的STBC是正交的。 這意味著STBC被設計成使得表示從編碼矩陣中取出的任何列對的矢量是正交的。 其結果是接收器處的簡單,線性,最佳解碼。 其最嚴重的缺點是,除了滿足此標準的一個代碼之外的所有代碼都必須犧牲其數據速率的某些比例(參見Alamouti的代碼)。
此外,存在準正交STBC,其以符號間干擾(ISI)為代價實現更高的數據速率。 因此,它們的差錯率性能受正交速率1 STBC之一的限制,正交速率1 STBC由於正交性而提供ISI自由傳輸。
STBCs的設計
STBC的設計基於Tarokh等人提出的所謂多樣性標準。在他們早期關於時空格線碼的論文中。 可以顯示正交STBC以實現該標準所允許的最大多樣性。
多樣性標準
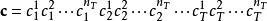 空時分組碼
空時分組碼撥打密碼
並調用錯誤解碼的接收碼字
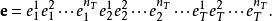 空時分組碼
空時分組碼然後是矩陣
 空時分組碼
空時分組碼 空時分組碼
空時分組碼 空時分組碼
空時分組碼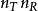 空時分組碼
空時分組碼 空時分組碼
空時分組碼 空時分組碼
空時分組碼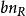 空時分組碼
空時分組碼必須為任何一對不同的代碼字和提供全等級,以便給出{的最大可能多樣性順序。相反,)對於不同碼字對的最小等級,則空時碼提供分集順序。對下面顯示的示例STBC的檢查表明它們都滿足該標準以獲得最大的多樣性。
編碼
Alamouti的代碼
西亞瓦什·阿拉穆蒂(Siavash Alamouti)在1998年發明了所有STBC中最簡單的,儘管他自己並沒有使用“時空分組碼”這個術語。它設計用於雙發射天線系統,並具有編碼矩陣:
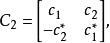 空時分組碼
空時分組碼其中*表示復共軛。
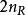 空時分組碼
空時分組碼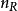 空時分組碼
空時分組碼很明顯,這是一個速率-1代碼。傳輸兩個符號需要兩個時隙。使用下面討論的最佳解碼方案,該STBC的誤碼率(BER)等於- 分支最大比率組合(MRC)。這是接收處理後符號之間完全正交的結果 - 每個符號傳送兩個副本,並且接收到個副本。
這是一個非常特殊的STBC。它是唯一達到率-1的正交STBC。也就是說,它是唯一能夠在不需要犧牲數據速率的情況下實現其全部分集增益的STBC。嚴格地說,這僅適用於複雜的調製符號。由於幾乎所有的星座圖都依賴於複數,因此該屬性通常使Alamouti的代碼比高階STBC具有顯著的優勢,即使它們實現了更好的錯誤率性能。有關詳細信息,請參閱“速率限制”。
Alamouti在1998年提出的建議的重要性在於它首次證明了一種編碼方法,它能夠在接收機上實現線性處理的完全多樣性。早期關於發射分集的提議需要處理方案,其與發射天線的數量成指數地縮放。此外,它是第一個具有這種能力的開環發射分集技術。隨後對Alamouti概念的概括已經對無線通信行業產生了巨大影響。
高階STBC
Tarokh等人。發現了一組特別簡單的STBC,並創造了該計畫的名稱。他們還證明,超過2個發射天線的代碼無法實現全速率。他們的代碼後來得到了改進(原作者和其他許多作者)。然而,它們作為速率無法達到1的明確例子,以及生產“好”STBC必須解決的其他問題。他們還展示了簡單的線性解碼方案,該方案在完全的信道狀態信息假設下與其代碼一致。
3個發射天線
3個發射天線的兩個直接代碼是:
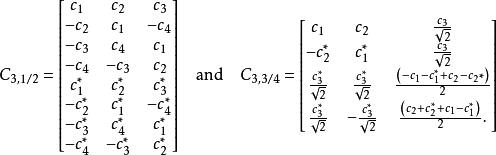 空時分組碼
空時分組碼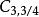 空時分組碼
空時分組碼這些代碼分別達到速率-1/2和速率-3/4。這兩個矩陣給出了為什麼兩個以上天線的代碼必須犧牲率的例子 - 這是實現正交性的唯一方法。的一個特殊問題是它傳輸的符號之間的功率不均勻。這意味著信號不具有恆定的包絡,並且每個天線必須傳送的功率必須變化,這兩者都是不希望的。此後,設計了克服此問題的此代碼的修改版本。
4個發射天線
4個發射天線的兩個直接代碼是:
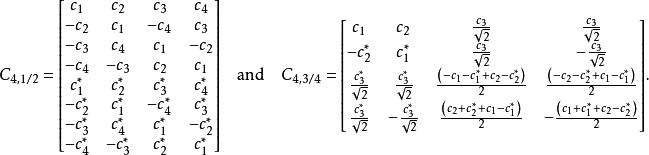 空時分組碼
空時分組碼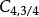 空時分組碼
空時分組碼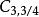 空時分組碼
空時分組碼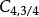 空時分組碼
空時分組碼這些代碼分別實現了速率-1 / 2和速率3/4,就像它們的3天線對應物一樣。表現出與相同的不均勻功率問題。的改進版本是
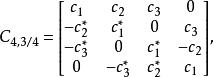 空時分組碼
空時分組碼它在所有時隙中具有來自所有天線的相等功率。
解碼
正交STBC的一個特別有吸引力的特徵是可以僅線上性處理的情況下在接收器處實現最大似然解碼。為了考慮解碼方法,需要無線通信系統的模型。
 空時分組碼
空時分組碼 空時分組碼
空時分組碼 空時分組碼
空時分組碼在時,在天線處接收的信號是:
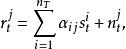 空時分組碼
空時分組碼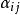 空時分組碼
空時分組碼 空時分組碼
空時分組碼 空時分組碼
空時分組碼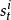 空時分組碼
空時分組碼 空時分組碼
空時分組碼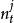 空時分組碼
空時分組碼其中是發射天線的路徑增益接收天線,是發射天線傳送的信號和是加性高斯白像的樣本噪音(AWGN)。
最大似然檢測規則是形成決策變數
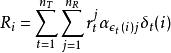 空時分組碼
空時分組碼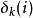 空時分組碼
空時分組碼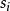 空時分組碼
空時分組碼 空時分組碼
空時分組碼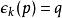 空時分組碼
空時分組碼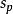 空時分組碼
空時分組碼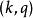 空時分組碼
空時分組碼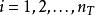 空時分組碼
空時分組碼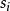 空時分組碼
空時分組碼其中是在第k行中的符號編碼矩陣,表示是(達到符號差異) ),編碼矩陣的元素,然後決定滿足的星座符號
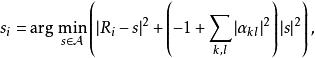 空時分組碼
空時分組碼 空時分組碼
空時分組碼用星座字母表。儘管它外觀,但它是一種簡單的線性解碼方案,可提供最大的多樣性。
準正交STBC
這些代碼表現出部分正交性,並且僅提供上述分集增益的一部分。 Hamid Jafarkhani報導的一個例子是:
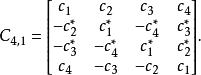 空時分組碼
空時分組碼正交性標準僅適用於列(1和2),(1和3),(2和4)和(3和4)。然而,至關重要的是,代碼是全速率的,並且仍然只需要在接收器處進行線性處理,儘管解碼比正交STBC稍微複雜一些。結果表明,該Q-STBC在良好的信噪比(SNR)範圍內優於(在誤碼率方面)完全正交的4天線STBC。然而,在高SNR下(在這種特定情況下高於約22dB),正交STBC提供的增加的分集產生更好的BER。除此之外,必須根據有用的數據吞吐量來考慮方案的相對優點。
從所示的基本示例開始,Q-STBC也得到了很大的進展。