玻耳茲曼方程數值解法

玻耳茲曼方程是原子物理、天體物理等領域中的描寫粒子(中子、質子、光子等)運動的基本微分－積分方程。假定粒子在兩次碰撞之間作等速直線運動，而在穿過介質的過程中按照一定的機率與其他粒子相碰撞，從而發生偏斜、慢化、被吸收或增殖等現象。求解玻耳茲曼方程，就是要求出在任一時刻，具有不同速度的粒子在空間的分布。

玻耳茲曼方程數值解法

正文

玻耳茲曼方程是原子物理、天體物理等領域中的描寫粒子(中子、質子、光子等)運動的基本微分－積分方程。假定粒子在兩次碰撞之間作等速直線運動，而在穿過介質的過程中按照一定的機率與其他粒子相碰撞，從而發生偏斜、慢化、被吸收或增殖等現象。由於粒子是大量的，因此可以忽略統計起伏，把它們看成是連續體。求解玻耳茲曼方程，就是要求出在任一時刻，具有不同速度的粒子在空間的分布。玻耳茲曼方程數值解法很多，其中以解描述中子輸運問題的玻耳茲曼方程的數值方法較為典型。
描述非定常中子輸運過程的玻耳茲曼方程為：

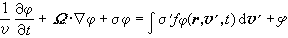, 　(1)

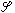式中t為時間；r、v分別為中子的位置和速度向量，v＝vΩ,Ω為中子速度方向的單位向量；φ(r,v,t)為中子角通量分布；σ(v,r)表示在點r處速度為v的中子的巨觀總截面，σ┡=σ(v┡,r);ƒ(v┡→v;r)dv是在r處中子速度由v┡轉移到v與v+dv之間的總機率；是獨立中子源。對於單速各向同性散射一維球對稱問題，非定常中子輸運方程為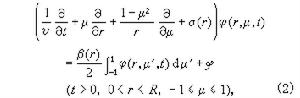

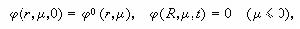
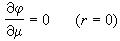式中r為徑向坐標;μ＝cosθ,θ為向徑和速度向量間的夾角；σ(r)為總截面；β(r)=σ(r)с(r)，с(r)為在r處每次碰撞所產生的平均次級中子數。方程(2)的定解條件為

。

20世紀40年代發展了用於解定常問題的兩類主要解法。
①球諧函式法 它把φ和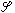按勒讓德多項式PN(μ)(球諧函式）展開，例如，令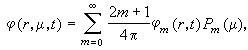

利用勒讓德多項式的性質，把方程簡化，再取展式的前N+1項,得φ0,φ1,…,φN的N+1個方程的聯立方程組,然後用差分法求數值解。該法又稱為PN近似法。
②威克－昌德拉塞卡離散縱標法 簡稱WC法。它(主要針對平板幾何問題)是取μ的一組固定值，μ0,μ1,…,μN，對φ(r,μi,t)(i=1,2,…,N)寫出方程組。右端積分用數值積分逼近，例如取μi為勒讓德多項式零點的高斯求積公式，然後用差分法求解。對於各向同性散射的平板問題，WC法和球諧函式法是等價的。
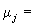
1953年 B.G.卡爾森提出了解中子輸運方程(2)的SN方法,該法取－1=μ0<μ1<…<μN=1（其中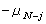）,把【-1,1】分成N個區間,在每個區間【μj-1,μj】上假定φ是μ的線性函式,同樣取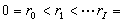R,假定在每個區間 【ri-1，ri】上 φ 也是 r 的線性函式。將(2)在區域{ri-1≤r≤ri,μj-1≤μ≤μj}上對r和μ積分，然後對時間作隱式向後差分得到差分格式，並適當選取插值公式，使差分方程的解滿足粒子數守恆的性質。
卡爾森等人在50年代末進一步提出離散SN法，又稱 離散縱標法(簡記DSN法)。這種方法可以比較容易地推廣到多維情況。它是從守恆方程

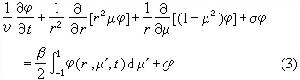
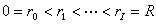出發的，離散分點取為 ，-1<μ1<μ2<…<μN<1，其中μ1，μ2，…，μN取為勒讓德多項式零點,取N為偶數，右端積分用高斯積分公式近似。在點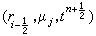上建立差分，為此在高斯積分係數ωj對應的子區間上對μ 近似積分，在(ri-1,ri)上對r作體積分，對t用中心差分，則得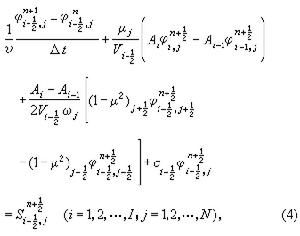

式中是以 ri-1和ri為內外半徑的球殼的體積，Ai是半徑為ri的球面面積。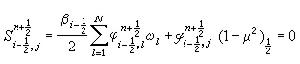

,

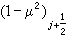按遞推公式

求出。此外，還要補充關係

和邊界(μ=-1)方程

定解條件離散化為
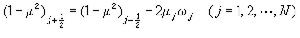
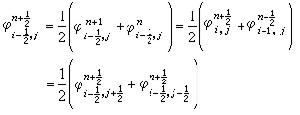
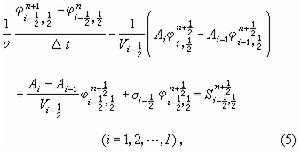
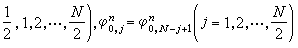。若取φn為疊代初值，把S中的φ用前次疊代值代入，則利用邊界條件，(4)、(5)可顯式遞推求解，計算步驟按μ從小到大的順序進行。當μ<0時,利用外邊界條件對r從大到小進行計算，當μ>0時，則利用中心對稱條件,對r從小到大進行計算。
SN方法和 DSN方法是求解玻耳茲曼方程的有效的數值方法，其主要缺點是計算中可能出現負通量，為了避免出現負通量有各種修正格式。
對於定常的玻耳茲曼方程，70年代出現了多種有限元算法。有通過引進角通量偶次分量，把方程化為自伴形式，再構造泛函求極小的有限元算法；也有直接用加廖金法（包括連續的和不連續的方法）和配置法等的有限元算法。
此外,還有許多其他的數值方法,例如特徵線法、分裂法和幾種方法相結合的混合解法，以及求解積分型輸運方程的各種數值方法。而基本機率理論的蒙特卡羅法在輸運計算中也占有重要的地位。
參考書目
　R.D.Richtmyer and K.W.Morton,Difference Method for Initialvalue Problems, 2nd ed.，Interscience, New York,1967.

配圖

相關連線