穆迪次序圖法的基本原理
通常，可供選擇的事物越多，選出最好的就越難。如果各種選擇之間有利方面和不利方面錯綜交叉在一起，要做出最終決策就更顯得困難重重。因為最簡單、最精確的選擇，產生於對兩種方案的直接對比中。所以在進行多方案（多因素）的比較時，不必同時比較兩種以上的方案，而只將諸方案（因素）兩兩比較並記分，然后綜合計分，即可得到以綜合計分表示事物間相對重要性的一個無偏見的次序序列，也就是得到一個從最優到最劣的方案次序。這種按從最優到最劣的次序給事物排隊的系統方法，可以套用於一系列的決策問題中。
穆迪次序圖法的主要內容及決策步驟
簡單次序圖
某公司對經營狀況進行分析後，發現有許多因素影響其效益。用次序圖對諸多因素進行評價，以確定影響管理效益的最主要因素。其主要步驟是：
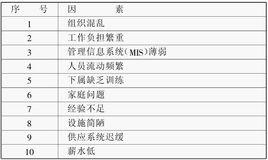
（1）、列出所有需要考慮的可能項目（因素），並編號、列表。設影響該公司效益的諸因素如下表。
表：因素一覽表
（2）、"構造空白次序圖。按因素的數目（n），編制 n×n矩陣圖。然後將因素代碼分別標在圖的左側和頂端，將從左上角到右下角的對角線上的方格塗黑，將問題寫在圖的上方，將因素的內容寫在圖的左方。
（3）進行因素比較。逐次進行因素間的兩兩比較，並將兩因素比較的結果按重要（優先）與否，記1或0分，並填在相應的空格里。如，從因素1和因素2的比較開始，假如我們認為“工作負擔繁重”比“組織混亂”影響更大，則因素2（“工作負擔繁重”）處於較優先的次序地位。即可在第1行第2列的方格里填0，在第2行第1列的方格里填1。
然後根據同理依次進行因素 1與其餘n—1個因素之間的比較，得到一個因素評價完成後的次序圖。
接下來，再進行因素2與其餘八個因素的逐一對比。例如，假定“工作負擔繁重”比“[font color=#800080]管理信息系統[/font]薄弱”對管理效率的影響較大，則2行3列填1，3行2列填0。這表明，因素2較因素3具有優先的次序。
依次進行因素3與其餘7個因素的對比。其餘按同理類推，最終可以得到所有因素之間兩兩比較的次序圖。整個圖填滿後，加總各行數值，並將其列在圖的右側。
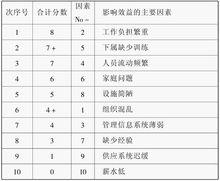
（4）因素排序。比較這些和數，和數最大的因素即為最優先的因素，和數次大的因素即為次優先的因素……，按照這個次序將所有的因素從最重要的到最不重要的逐一排列起來（見下表）。
穆迪次序圖法當兩個因素的和數相等時，就應比較這兩個因素，兩者間次序優先者，則排序在前，其和數後注“+號。
當三個以上因素的和數相等時，則需要構造這幾個因素的子次序圖，確定這幾個因素的次序。
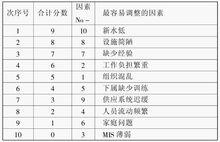
以上是按照影響管理效益的重要性確定的次序。如果把問題改為“為提高管理效益，哪個因素最容易調整？”施行前面一樣的過程，可以得到新的次序圖和新的排序。
穆迪次序圖法復投入次序圖
在進行因素的兩兩比較時，參與決策者（與會者或評價小組）的意見往往不一致，則可以採用復投入次序圖，更準確地反映各參與決策者的意見。
例如一個企業要按次序排列其計畫的12個工程項目，確定成功可能性最小的項目，並最終取消成功可能性最小的三個項目，以便壓縮開支。假定參與決策者有 5人。在畫出空白次序圖後，開始項目間的兩兩比較。如比較 A、B之間成功的可能性時，3人認為 A可能性小，2人認為 B可能性小，則在行2列填3，2行1列填2。
依同理進行其他項目的比較，得到全部項目比較完成以後的復投入次序圖和按優先次序排列的項目序列。
穆迪次序圖法由次序可知，F為應取消的項目。去掉 F後，再做一次比較，可以確定 A是否為第二個應該被取消的項目。
復投入次序圖的一種變形，叫作加權次序圖。比如在前述例子中，參與決策的 5個人中，有 4個是部門領導，1個是總經理，則總經理的意見有較大的權數。若記總經理表決票為3分，則其他人表決票各為 1分。若認為 A成功的可能性小的3人中有總經理，則應在1行2列上填5，2行1列上仍填2。其餘同理類推。
組合次序圖。
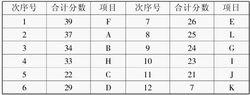
如果考慮的問題不止一個，即要確定優先順序的問題不止一個，則可利用組合次序圖。例如我們在管理效益的分析中，對兩個問題，哪個因素影響最大和哪個問題最易調整給予同等的關心。這時確定組合優先順序表的方法是，首先做好預備次序圖，然後對它們的結果進行數字加總，再確定順序（如下表）
表：預備的組合次序表
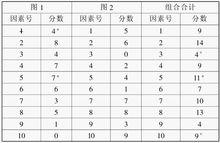穆迪次序圖法其中，“+”意義同前。“關”表示在相等的合計分數中，其因素在某一問題中有較高的分數。根據組合合計分數，可得組合次序表（如下表）
表：組合次序表
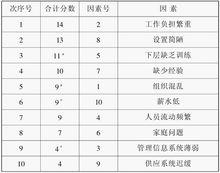穆迪次序圖法組合次序圖的一種變形，是加權組合次序圖。當考慮的兩個問題中，意義並不相同時，則較為重要的一個應具有較大的權數。如在前述問題中，哪個因素最易調整比哪個因素影響最大的問題具有雙倍的重要性，則應對因素最易調整的分數加權（在分數上乘2），然後再求和，確定次序。
穆迪次序圖法的作用
穆迪次序圖是一種有價值的決策工具，但它並不能代替決策。次序圖易記易行，可以在決策中較好地發揮作用，如：在工作人員的評價、職位功能評價、[font color=#0000ff]項目評價[/font]、安排日常工作、優選最佳工作等等方面都可以使用。
