簡介
稀疏濾波方法的核心思想就是避免對數據分布的顯式建模,而是最佳化特徵分布的稀疏性從而得到好的特徵表達。
一般來說,大部分的特徵學習方法都是試圖去建模給定訓練數據的真實分布。換句話說,特徵學習就是學習一個模型,這個模型描述的就是數據真實分布的一種近似。這些方法包括denoising autoencoders,restricted Boltzmann machines (RBMs),independent component analysis (ICA)和sparse coding等等。
這些方法效果都不錯,但缺點就是,他們都需要調節很多參數。比如說學習速率learning rates、動量momentum(好像rbm中需要用到)、稀疏度懲罰係數sparsity penalties和權值衰減係數weight decay等。而這些參數最終的確定需要通過交叉驗證獲得,本身這樣的結構訓練起來所用時間就長,這么多參數要用交叉驗證來獲取時間就更多了。我們花了大力氣去調節得到一組好的參數,但是換一個任務,我們又得調節換另一組好的參數,這樣就會花了俺們太多的時間了。雖然ICA只需要調節一個參數,但它對於高維輸入或者很大的特徵集來說,拓展能力較弱。
稀疏濾波一種簡單並且有效的特徵學習算法,它只需要最少的參數調節。雖然學習數據分布的模型是可取的,而且效果也不錯,但是它往往會使學習的算法複雜化,例如:RBMs需要近似對數劃分log-partition函式的梯度,這樣才可能最佳化數據的似然函式。Sparse coding需要在每次的疊代過程中尋找活躍的基的係數,這是比較耗時的。而且,稀疏因子也是一個需要調整的參數。本文方法主要是繞過對數據分布的估計,直接分析最佳化特徵的分布。了解最優特徵分布需要先關注特徵的一些主要屬性:population sparsity,lifetime sparsity和high dispersal。怎樣的特徵才是好的特徵,才是對分類或者其他任務好的特徵。我們的學習算法就應該學會去提取這種特徵。
具體介紹
 稀疏濾波
稀疏濾波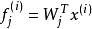 稀疏濾波
稀疏濾波稀疏濾波是如何捕捉到上面說的那些特性的。我們先考慮下從每個樣本中計算線性特徵。具體來說,我們用 來表示第i個樣本(特徵矩陣中第i列)的第j個特徵值(特徵矩陣中第j行)。因為是線性特徵,所以 。第一步,我們先簡單的對特徵矩陣的行進行歸一化,然後再對列進行歸一化,然後再將矩陣中所有元素的絕對值求和。
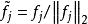 稀疏濾波
稀疏濾波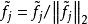 稀疏濾波
稀疏濾波具體來說,我們先歸一化每個特徵為相等的激活值。具體做法是將每一個特徵除以其在所有樣本的二範數: 。然後我們再歸一化每一個樣本的特徵。這樣,他們就會落在二範數的單位球體unit L2-ball上面了。具體做法是: 。這時候,我們就可以對這些歸一化過的特徵進行最佳化了。我們使用L1範數懲罰來約束稀疏性。對於一個有M個樣本的數據集,sparse filtering的目標函式表示為:
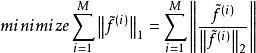 稀疏濾波
稀疏濾波最佳化樣本的稀疏性
 圖一
圖一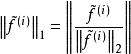 稀疏濾波
稀疏濾波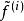 稀疏濾波
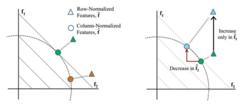
稀疏濾波其中 這一項度量的就是第i個樣本的特徵的population sparsity,也就是限制每個樣本只有很少的非零值。因為歸一化的特徵 被約束只能落在二範數的單位球體上面,所以當這些特徵是稀疏的時候,也就是樣本接近特徵坐標軸的時候,上面的目標函式才會最小化。反之,如果一個樣本的每個特徵值都差不多,那么就會導致一個很高的懲罰。可能有點難理解,我們看圖一:
圖一左:假設我們的特徵維數是兩維(f1, f2),我們有兩個樣本,綠色和褐色的。每個樣本都會先投影到二範數的球體上面(二維的話就是單位圓),再進行稀疏性的最佳化。可以看到,當樣本落在坐標軸的時候,特徵具有最大的稀疏性(例如,一個樣本落在f2軸上,那么這個樣本的表示就是(0, 1),一個特徵值為1,其他的為0,那么很明顯它具有最大的稀疏性)。圖一右:因為歸一化,特徵之間會存在競爭。上面有一個只在f1特徵上增加的樣本。可以看到,儘管它只在f1方向上增加(綠色三角型轉移到藍色三角型),經過列歸一化後(投影到單位圓上),可以看到第二個特徵f2會減少(綠色圓圈轉移到藍色圓圈)。也就是說特徵之間存在競爭,我變大,你就得變小。
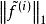 稀疏濾波
稀疏濾波對特徵進行歸一化的一個屬性就是它會隱含的進行特徵間的競爭。歸一化會使得如果只有一個特徵分量f增大,那么其他所有的特徵分量的值將會減小。相似的,如果只有一個特徵分量f減小,那么其他所有的特徵分量的值將會增大。因此,我們最小化 ,將會驅使歸一化的特徵趨於稀疏和大部分接近於0。也就是,一些特徵會比較大,其他的特徵值都很小(接近於0)。因此,這個目標函式會最佳化特徵的population sparsity。
最佳化高擴散性
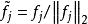 稀疏濾波
稀疏濾波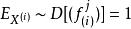 稀疏濾波
稀疏濾波上面說到,特徵的high dispersal屬性要求每個特徵被恆等激活。在這裡,我們粗魯地強制每個特徵的激活值平方後的均值相等。在上面sparse filtering的公式中,我們首先通過將每個特徵除以它在所有樣本上面的二範數來歸一化每個特徵,使他們具有相同的激活值: 。實際上,它和約束每個特徵具有相同的平方期望值有一樣的效果。 ,因此,它已經隱含的最佳化了high dispersal屬性。
最佳化稀疏性
我們發現,對population sparsity和high dispersal的最佳化就已經隱含的最佳化了特徵的lifetime sparsity。這其中的緣由是什麼呢。首先,一個具有population sparsity的特徵分布在特徵矩陣里會存在很多非激活的元素(為0的元素)。而且,因為滿足high dispersal,這些零元素會近似均勻的分布在所有的特徵里。因此,每一個特徵必然會有一定數量的零元素,從而保證了lifetime sparsity。所以,對於population sparsity和high dispersal的最佳化就已經足夠得到一個好的特徵描述了。
深度稀疏濾波
因為sparse filtering的目標函式是不可知的,我們可以自由地選擇一個前向網路來計算這些特徵。一般來說,我們都使用比較複雜的非線性函式,例如:
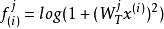 稀疏濾波
稀疏濾波或者多層網路來計算這些特徵。這樣,sparse filtering也算是訓練深度網路的一種自然的框架了。
有sparse filtering的深度網路可以使用有代表性的逐層貪婪算法來訓練。我們可以先用sparse filtering來訓練得到一個單層的歸一化的特徵,然後用它當成第二層的輸入去訓練第二層,其他層一樣。實驗中,我們發現,它能學習到很有意義的特徵表達。
與divisive normalization的聯繫
sparse filtering的population sparsity和divisive normalization有著緊密的聯繫。divisive normalization是一種視覺處理過程,一個神經元的回響會除以其鄰域所有神經元的回響的和(或加權和)。divisive normalization在多級目標識別中是很有效的。然而,它被當成一個預處理階段引入,而不是屬於非監督學習(預訓練)的一部分。實際上,sparse filtering把divisive normalization結合到了特徵學習過程中,通過讓特徵間競爭,學習到滿足population sparse的特徵表達。