秩定域判別法(又稱梁氏判別法)
秩定域判別法由我國學者梁燁提出,用於已知樣本分類和大量指標時,通過逐一分析單一指標對樣本分類進行解釋的判別方法。
基本思路秩定域模型的基本思路是以秩序確定閾值。即對某一指標Q1進行排序,若已知類別出現集中趨勢,則可確定閾值Yq1,使得以指標Q1以閾值Yq1為界被判為兩類。
例1秩定域模型示例1
| 指標Q1 | 指標Q1的秩序值 | 所屬類別 | |
| 樣本1 | 1.72 | 2 | 1 |
| 樣本2 | 1.50 | 1 | 1 |
| 樣本3 | 3.50 | 3 | 2 |
| 樣本4 | 4.14 | 4 | 2 |
對於大多樣本,使用上面的方法進行分析時指標並不會有非常絕對的集中趨勢,中間可能含有混雜。如
Table 2.2秩定域模型示例2
| 指標Q1 | Q1的秩 | 指標Q2 | Q2的秩 | 所屬類別 | |
| 樣本1 | 1.72 | 2 | 10 | 3 | 1 |
| 樣本2 | 1.50 | 1 | 6 | 1 | 1 |
| 樣本3 | 1.98 | 4 | 12 | 6 | 1 |
| 樣本4 | 1.97 | 3 | 11 | 5 | 2 |
| 樣本5 | 3.50 | 5 | 10 | 3 | 2 |
| 樣本6 | 4.14 | 6 | 6 | 1 | 2 |
此時使用一次秩定域模型無法將樣例判斷為理想類別,應採用多次秩定域模型加以判定。
多次秩定域判定的基本方法是:
步驟一:找到一個閾值Yqn,對於Qn,可以將全部的某一類別分到的值Yqn同側,而在這一側的其他類別混雜含量Hn最少,將這一側樣本命名為“準分類集”,另一側的樣本命名為“待定樣本集”。
步驟二:對於“準分類集”中的樣本,重新使用步驟一進行判別,直到準分類集中只剩下一個類別。排除的樣本被棄入待定樣本集。
如例2中,n=1時,可以使用Yq1=2.74將第一類完全分到Yq1同側,而這一側H1=1。n=2時,不存在Yq2將類別完全分開,故被排除選擇。此時Q1< Yq1的樣本被納入“準分類集”,其他樣本被納入“待定樣本集”。
對於“準分類集”內的樣本,重新使用多次秩定域判定的步驟一,可以找到Yq2=8將混雜樣本去除。因此最終得到例2的秩定域判別結果如圖:
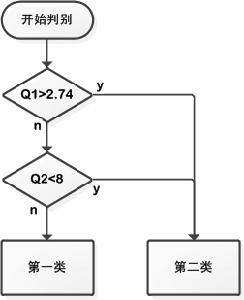 分類結果
分類結果