基本介紹
秦九韶方法亦稱霍納法則,是計算多項式值的簡便方法。設多項式
f(x)=ax+…+ax+a,
為計算f(x)的值可令
f(x)=p(x)(x-x)+f(x),
其中
p(x)=bx +…+bx+b.
比較上式兩邊x的同次冪係數,則得
b=a,
b=a+xb(i=1,2,…,n),
f(x)=b,
這就是 秦九韶方法,計算一個n次多項式的值只用n個乘法和n個加法運算,它也可表示為
f(x)=(…((ax+a)x+a)x+…+a)x+a,
這種算法計算量少,程式簡單,並且若對p(x)再用同樣算法令
c=b,c=b+xc(i=1,2,…,n-1),
則得f′(x)=c。
相關介紹
類似上面敘述的,可求出各階導數值。秦九韶於1247年在《數書九章》中,第一次用上述方法計算高次方程的函式值,並通過逐次變換與累試,使最後某個累試值x,計算出的b=f(x)=0為止。秦九韶給出的例題都是求正實根,為說明他的求根方法,用現代數學記號並以n=3為例加以說明 ,設
f(x)=ax³+ax²+ax+a,
若x為一近似根,用x-x除,相當於在x處作泰勒展開
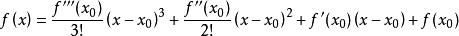 秦九韶方法
秦九韶方法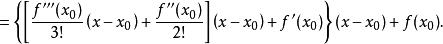 秦九韶方法
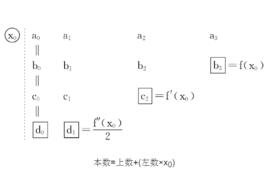
秦九韶方法秦九韶的計算公式用表格表示如下:
 秦九韶方法 秦九韶方法 | 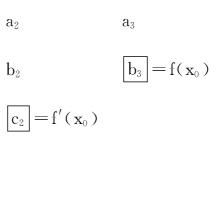 秦九韶方法 秦九韶方法 |
這裡計算規則是:
本數=上數+(左數×x)
而f(x)在x的泰勒展開式就是
f(x)=d(x-x)³+d(x-x)²+c(x-x)+b.
例如,求x³-67x²+1494x-11086=0的根。先估出近似x=20。
 秦九韶方法
秦九韶方法令y=x-20,方程變為f(y)=y³-7y²+14y-6,估計y=3,計算
 秦九韶方法
秦九韶方法因b=0,故f(y)=0的根為y*=3,代入x*=y*+20=23,即f(x)=0的根為x*=23,這就是秦九韶法的計算步驟,但秦九韶法通常是指他的計算高次多項式的算法,它比霍納(W.G.Horner)於1819年提出的同一算法早570多年 。