不同投影方法特點
中心投影雖立體感強，但線量度量困難，不宜於工程製圖，故只在解求角值或表示岩層裂隙密度等問題時選用，如以球面上某點為投影中心的球面透視投影。平行投影具有平行於投影面的直線和角度投影后其大小不變、平行直線的投影仍然是平行直線、直線上各線段之比等於其投影之比的性質，既適於繪製空間物體圖象，又便於度量，故在礦體幾何工作中廣泛選用，如標高投影、軸測投影和仿射投影等。
標高投影
採用零水平面作投影平面，將空間物體特徵點垂直投影於此投影平面上，用以確定各特徵點的平面位置(即點的x坐標和y坐標)，然後於此投影點旁用數字註明該空間點到投影面的距離(高程)的直角平行投影。
軸測投影
空間物體連同坐標軸一起投影於投影面上，利用三個坐標軸確定物體三個尺度的一種平行投影。軸測投影中，平行於某一坐標軸的所有線段，其投影變形係數相同。
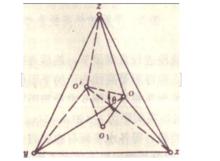礦體幾何投影變形係數是空間某線段沿某一坐標軸的投影長與其沿相應坐標軸的實長之比。圖1中，o′x、o′y、o′z為空間直角坐標軸，ox、oy、oz為斜角軸測投影軸，投影方向o′o與投影面的夾角為θ。若以p=ox/o′x、q=oy/o′y、r=oz/o′z相應地表示在x、y、z軸向上的變形係數，則變形係數間有如下關係：
p+q+r=2+ctgθ
根據變形係數p、q、r及投影方向與投影面間的夾角θ之不同，軸測投影可按下表分類。
| θ p.q.r | 直角軸測投影θ=90° | 斜角軸測投影θ≠90° |
| 等測 二測 三測 | p=q=r p=q或p=r或q=r p≠q≠r | p=q=r p=q或p=r或q=r p≠q≠r |
仿射投影
利用仿射投影變換法將主物面上的物體圖形射影於投影面上的一種平行投影，是軸測投影的一種特殊情形。依據物體圖形在不同水平上特徵點的坐標變換為對應的仿射坐標，而獲得該物體圖的立體圖象。圖1中，H為主物面，P為投影面，兩平面的夾角為ψ，兩平面的交線ox取作仿射橫軸ox′，在P平面上與ox′垂直的方向取作仿射縱軸oy′。S為射影方向。若主物面H上有三角形ABC，按射影方向S射影於投影面P上，得對應三角形A′B′C′。這樣的變換稱作仿射變換。過兩對應直線AB與A′B′、AC與A′C′、BC與B′C′的平面將與主物面及投影面分別相交於點a、b、c，且這些點均必在仿射橫軸ox′上，即三角形對應邊延長時將相交於仿射橫軸上的一點。依投影方向與投影面的關係，仿射投影分為直角仿射投影與斜角仿射投影。當投影方向垂直於投影面時，稱作直角仿射投影，否則稱作斜角仿射投影。在斜角仿射投影中，若投射方向與仿射軸正交，則稱作與仿射軸正交的斜角仿射投影;若投射方向與仿射軸斜交，則稱作任意斜角仿射投影。在礦體幾何學中多選用直角仿射投影和與仿射軸正交的斜角仿射投影。任意斜角仿射投影很少採用。
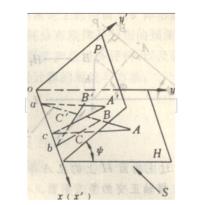礦體幾何投影