歷史背景
如同前面所述，真空電容率是一個度量系統常數。它的出現於電磁量的定義方程，主要是因為一個稱為理想化的程式。只使用純理論的推導，麥克斯韋方程組奇異地預測出，電磁波以光速傳播於自由空間。繼續推論這個預測，就可以給出的數值。若想了解為什麼會有這數值，必須稍微閱讀一下電磁度量系統的發展史。（詳見詞條：電磁學）
在以下的講述中，請注意到我們經典物理並不特別區分“真空”和“自由空間”這兩個術語。當今文獻里，“真空”可能指為很多種不同的實驗狀況和理論實體。在閱讀文獻時，只有上下文可以決定術語的含意。
基本概念
真空介電常數
，又稱為真空電容率，或稱電常數，是一個常見的電磁學物理常數，符號為 ε0。在國際單位制里，真空介電常數的近似數值為：
ε= 8. 854187817 × 10F/ m；
真空介電常數是物理量在度量時引進的常數( 主要是庫侖定律中對電荷量的度量) ，根據麥克斯韋方程組，可推知真空介電常數與其它物理常數的關係。
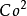真空介電常數ε=1/(μ
)
其中，c是光波傳播於真空的光速，μ是真空磁導率。上式可作為真空介電常數的定義式。
與真空背景周期的關係
值得一提的是，t =8.81 ×10秒在數值上剛好近似等於真空介電常數ε，這兩個量之間有什麼關係呢? 為了說明這個問題，這裡假定真空中有二個帶有相同電量( 電量為 e) 的點電荷相互作用，相互作用勢能為
Ep=e/ε4πr
如果單個電荷以周期 t 做圓周運動，則電流強度為 I = e/t. 根據實驗結果，電阻的表達式可寫為：
R = ρl/s
其中 ρ 為電阻率，l 為介質的長度，s 為介質的橫截面積，電流的方向垂直於橫截面。對兩個點電荷來說，雖然它們“靜止”，但它們受“真空背景溫度”的影響，也在做輕微的熱運動，這個運動可看成是簡諧運動( 也可用圓周運動來進行描述) ，運動方向在兩個點電荷之間，周期為( 即前面的所說的“真空背景周期”)。運動電荷對應的電流可認為就是位移電流，這種運動使兩個電荷間的電場也發生了周期性的變化，變化的周期也為t. 由於位移電流的本質就是變化的電場，則 e/t 在數值上可表示電流的空間分布，電流方向垂直於以 r 為半徑的球面，(5) 式中的橫截面積為 s =4πr2.
由於系統處在真空之中，電阻率很大(相對於導體來說) ，但電子的運動是自由的，兩個點電荷間的電阻為：
R = ρr/4πr= ρ1/4πr
一個電荷相對一另一個電荷的電勢 U = IR = ρe/t·1/4πr，相對應的電勢能為
Ep= eU = ρ.e/t4πr
比較勢能表達式( 4) 式和( 6) 式可知 ε0= t / p，表明真空介電常數 ε0與真空背景周期成正比. 如果假定電阻率 ρ =1，真空背景周期與真空介電常數在數值上完全相等. 根據( 3) 式得：
ε=h/2KTρ
上式說明真空背景溫度與真空介電常數成反比，這個結果也顯示現實真空環境與宇宙背景有直接關係.雖然用 e/t 來表示位移電流的空間分布並不嚴格，但是足以說明真空介電常數的測量值與宇宙背景溫度有很大程度的關聯。
單位理想化
查爾斯·庫侖和其它物理學家的實驗，證明庫侖定律：分開距離為r，電量都是q的兩個點電荷，其相互作用於對方的力F，可以用方程表達為
；
其中，是個常數。
假若，對其它變數不加以任何約束，則可以任意地設定。對於每一個不同的數值設定，的詮釋也相隨地不同。為了要避免混淆不清，每一個不同的詮釋必須有不同的名稱和標記符號。
厘米-克-秒靜電制是一個十九世紀後期建立的標準系統。在這標準系統里，常數的數值被設定為 1 ，電荷量的量綱被稱為高斯電荷量。這樣，作用力的方程變為
；
其中，是高斯電荷量。
假設兩個點電荷的電荷量都是一個單位高斯電荷量，分隔距離是 1 厘米。則兩個點電荷相互作用於對方的力是 1達因。那么，高斯電荷量的量綱也可以寫為“達因厘米”。 這與國際單位制的量綱，“牛頓米”，有同樣的量綱。但是，高斯電荷量與國際單位制電荷量的量綱並不相同。高斯電荷量不是用庫侖來測量的。
後來，科學家覺得，對於球幾何案例，應該加入因子於庫侖定律，表達方程為
；
其中，、分別為新的常數和電荷量。
這個點子稱為理想化。設定。電量單位也改變了，但是，電量的量綱仍舊是“達因厘米”。
下一個步驟是將電量表達為一個獨自的基本物理量，標記為，將庫侖定律寫為它的現代形式：
。
很明顯地，舊厘米-克-秒靜電制里的電量與新的國際標準制電量的關係式為
。
