簡介
相對論波動方程預測了粒子在高能量和速度下的行為,與光速相當,確定了量子場的動力學,常套用在相對論量子力學、粒子物理學等。
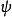 相對論性波動方程
相對論性波動方程方程的解通常表示為 (希臘語psi),在相對論量子力學中被稱為“波函式”,在量子場論中被稱為“場”。由於它們具有波動方程的數學形式或者由拉格朗日密度和場理論的歐拉 - 拉格朗日方程生成,因此方程本身被稱為“波動方程”或“場方程”。
在薛丁格圖中,波函式或場是薛丁格方程的解:
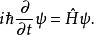 相對論性波動方程
相對論性波動方程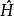 相對論性波動方程
相對論性波動方程上述是量子力學的一個假設。所有 相對論性波動方程可以通過指定各種形式的哈密頓算符 構造來描述量子系統。或者,費曼路徑積分公式中使用拉格朗日運算元而不是哈密頓運算元。
更一般地,相對論波動方程背後的現代形式主義是洛倫茲群理論,其中粒子的自旋與洛倫茲群的表示相對應。
方程
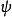 相對論性波動方程
相對論性波動方程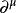 相對論性波動方程
相對論性波動方程以下等式具有滿足疊加原理的解,即波函式是加性的。在整個過程中,使用了張量指數表示法和Feynman斜線表示法的標準慣例,包括希臘指數,其中空間分量取值1,2,3,索引量的時間分量取0。波函式被表示為 , 是部件的四梯度運算元。
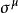 相對論性波動方程
相對論性波動方程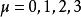 相對論性波動方程
相對論性波動方程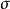 相對論性波動方程
相對論性波動方程在矩陣等式中,泡利矩陣被表示為 ,其中 ,其中 是2×2單位矩陣:
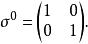 相對論性波動方程
相對論性波動方程其他矩陣有其一般的表示,表達式
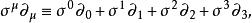 相對論性波動方程
相對論性波動方程是一個2×2矩陣運算元,作用於雙分量旋量場。
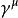 相對論性波動方程
相對論性波動方程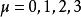 相對論性波動方程
相對論性波動方程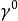 相對論性波動方程
相對論性波動方程伽瑪矩陣表示為 ,其中 ,有許多方式方式可以選擇,矩陣 是不一定是4×4單位矩陣,表達式:
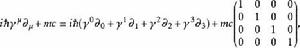 相對論性波動方程
相對論性波動方程是一個4×4矩陣運算元,作用於4分量的旋量場。
相關術語
•狹義相對論
•標量場
•洛倫茲變換
