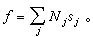簡介
phase space又稱相空間、Γ空間。對於一個具有s個自由度的力學系統，其運動狀態可用廣義坐標q1、q2、…、qs和廣義動量p1、p2、…，ps描述，把2s個p和q取作直角坐標，構成的2s維空間就是相宇。相宇中的一點稱為相點，代表系統的一種可能的運動狀態。隨著系統運動狀態的改變，相點在相宇中相應地描繪出一條軌跡。這裡的相是指運動狀態，與相變毫無關係。相宇概念是美國物理學家J.W.吉布斯在1902年引入的。
詳解
phase space或稱相空間，是經典的系綜理論中為了描述系統的微觀狀態而引入的一個基本概念。
考慮 N個同種粒子組成的巨觀力學系統,設每個粒子的自由度為 s，則系統自由度為 f= Ns。若系統中包含了若干種粒子,其中第 j種粒子的數目是 Nj，自由度是 sj，那么系統在某一給定時刻的微觀運動狀態決定於 f個廣義坐標 qi( i=1，2，… f)和相應的 f個廣義動量 pi( i=1,2,… f)在該時刻的數值。把這 f個 qi和 f個 pi取作坐標軸，就構成了一個2 f 維空間，稱為相宇或相空間,又叫Γ空間。這個名字是美國物理學家J.W.吉布斯於1902年引入的。這裡“相”的意思是指運動狀態。由於每一個坐標和其共軛動量的乘積具有能量乘時間的量綱，所以相空間體積元的量綱應是能量和時間乘積的 f次方。可以選擇不同的坐標描述同一個系統,而對同一系統的兩種不同的相空間，其體積元的量綱是相同的。並且,可以證明，在不同坐標系構成的相空間中,相同數目的代表點占據相同的體積。
相空間中的每一點，代表系統一種可能的運動狀態，系統的不同運動狀態，可以用相空間中不同的點來代表。每個系統有自己特有的相空間。從經典力學可知，系統的運動狀態隨時間變化，因此相空間中代表系統運動狀態的點將在相空間中移動，其軌道由哈密頓正則方程 確定，式中 H( q1,…, q; p1,…, p)是系統的哈密頓量。當系統從不同的初始狀態出發隨時間變化時，相空間中系統的代表點就沿不同的軌道運動。因哈密頓函式及其微分是單值函式，這些不同的軌道彼此不能相交。
