簡介
直線透視一種基本幾何元素的透視.直線的透視在一般情況下仍為直線;因為通過直線上各點的視線形成一個平面,這個平面與畫面的交線,即為直線的透視.當直線通過視點時,其透視為一點;直線位於畫面上時,其透視即其本身;直線位於一個通過視點且平行於畫面的平面內時,其透視在畫面上無限遠處.
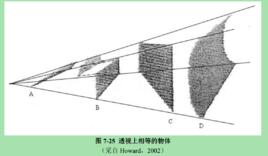
直線透視產生了一系列透視上的相等物體,如圖上圖所示。直線透視可以作為一種距離線索。 19 世紀中葉,克拉克、史密斯和瑞伯( Clark, Smith 和 Rabe, 1955)通過實驗驗證了這一點。他們在黑暗的背景中,向被試呈現了一個明亮的梯形,結果被試將梯形報告為有一邊(梯形的短邊)向遠處傾斜的矩形,這是由於梯形
上下兩邊長短不一,從而產生兩條平行線向遠處延伸的感覺。
歷史與發展
直線透視原理在古代就已經被發現了,所以中世紀及後來文藝復興時期的畫家都利用這個原理在平面上表現出空間關係。德國著名畫家達萊( Dürer, 1525)最早提出直線透視關係的數學原理。 17 世紀畫家杜布爾( Dubreul, J.)根據達萊的數學分析透視原理,用蝕刻畫製成樣板畫,以此來教授他的學生。下圖就是杜布爾的蝕刻畫,圖中所有的平行線都被畫得向遠處某點會聚,這使我們產生了長廊向遠處延伸的感覺 。
 杜布爾的蝕刻畫
杜布爾的蝕刻畫幾何透視
幾何透視( geometrical perspective)是指平面上的刺激物,根據視角原理,近處的對象面積大,占的視角大,看起來較大;遠處的對象占的視角小,看起來較小。幾何透視是日常生活中最常使用的距離物理線索。幾何透視主要包括直線透視、大小透視、視野中高度、紋理梯度 。