方法簡介
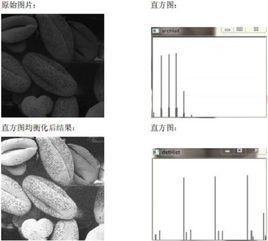
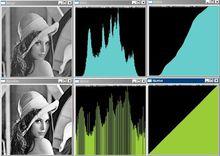 直方圖均衡
直方圖均衡直方圖均衡化通常用來增加許多圖像的全局對比度,尤其是當圖像的有用數據的對比度相當接近的時候。通過這種方法,亮度可以更好地在直方圖上分布。這樣就可以用於增強局部的對比度而不影響整體的對比度,直方圖均衡化通過有效地擴展常用的亮度來實現這種功能。
這種方法對於背景和前景都太亮或者太暗的圖像非常有用,這種方法尤其是可以帶來X光圖像中更好的骨骼結構顯示以及曝光過度或者曝光不足照片中更好的細節。這種方法的一個主要優勢是它是一個相當直觀的技術並且是可逆操作,如果已知均衡化函式,那么就可以恢復原始的直方圖,並且計算量也不大。這種方法的一個缺點是它對處理的數據不加選擇,它可能會增加背景噪聲的對比度並且降低有用信號的對比度。
直方圖均衡技術將原始圖像的灰度直方圖從比較集中的某個灰度區間變成在全部灰度範圍內的均勻分布, 由於其算法簡單, 無需藉助外來因素的參數設定,可以自成系統的運行, 有效地增強圖像對比度, 是一種常用的圖像增強方法. 一直以來, 直方圖均衡技術受到各個領域的重視, 比如在消費類電子產品鄰域, 在均衡圖像的同時希望保持圖像的亮度信息 。
實現過程
我們來看一個灰度圖像,讓 ni表示灰度 i出現的次數,這樣圖像中灰度為 i 的像素的出現機率是
L 是圖像中所有的灰度數, n 是圖像中所有的像素數, p 實際上是圖像的直方圖,歸一化到 0..1。
把 c 作為對應於 p 的累計機率函式, 定義為:
c 是圖像的累計歸一化直方圖。
我們創建一個形式為 y = T( x) 的變化,對於原始圖像中的每個值它就產生一個 y,這樣 y 的累計機率函式就可以在所有值範圍內進行線性化,轉換公式定義為:
yi = T( xi) = c( i)
注意 T 將不同的等級映射到 0..1 域,為了將這些值映射回它們最初的域,需要在結果上套用下面的簡單變換:
上面描述了灰度圖像上使用直方圖均衡化的方法,但是通過將這種方法分別用於圖像RGB顏色值的紅色、綠色和藍色分量,從而也可以對彩色圖像進行處理。
算法分類
全局直方圖均衡算法
傳統直方圖均衡算法利用一個變換函式將輸入圖像的灰度級映射到輸出圖像, 使輸出圖像各灰度級相對均勻分布, 從而圖像的對比度得到增強。
局部直方圖均衡算法
與全局方法相比, 局部直方圖均衡方法可以更好地增強圖像的局部細節. 局部方法可以分為子塊不重疊、子塊重疊與子塊部分重疊(POSHE)三種方法。
基於分頻和融合的直方圖均衡算法
考慮到將圖像的高頻分量和低頻分量分開,對低頻分量進行直方圖均衡處理, 對高頻分量進行線性加權增強, 再將兩者融合, 就可以避免直方圖均衡算法導致圖像細節信息丟失和噪聲放大的問題.
彩色圖像直方圖均衡算法
計算機視覺和計算機圖形學的發展使得彩色圖像和視頻得到廣泛套用, 對彩色圖像進行直方圖均衡的研究也越來越多, 現有的幾種彩色圖像直方圖增強方法有如下幾種:
(1) R、G、B 三幅子圖像分別均衡併合並
灰度圖像通過直方圖均衡算法可以很好地達到對比度增強的效果, 但針對具有三個分量的彩色圖像,通過簡單的對R、G、B三幅子圖像分別均衡及合併, 會使均衡後的圖像出現嚴重的色彩失真現象, 其主要原因在於傳統直方圖均衡算法過度地增強了圖像的亮度.因此, 採用這種方法進行彩色圖像直方圖均衡首要目標是增強圖像對比度時保持圖像的亮度均值.
(2) 根據聯合機率密度進行均衡
直接對彩色圖像進行處理, 計算 R、G、B 三幅子圖像的聯合機率密度函式, 並根據聯合機率密度函式進行直方圖均衡計算, 這種方法雖然一定程度消除了色彩失真的現象, 但是卻因需要計算聯合機率密度函式加大了算法的複雜度, 運算十分困難.
(3) HSI 模型對亮度分量進行均衡
這種方法將彩色圖像從RGB彩色模型轉化到HIS彩色模型, 然後對亮度分量I進行直方圖均衡增強, 再還原到 RGB 模型中, 該方法使均衡次數從 3 次簡化到1 次, 但是需要對圖像進行彩色模型的相互轉化, 仍需要一定的計算量, 並且增強後的圖像也會存在過增強的現象。