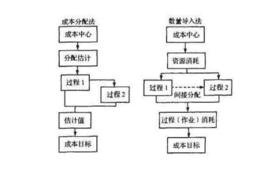
方法介紹
直接分配法(direct allocation method)是指在各輔助生產車間發生的費用,直接分配給輔助生產以外的各受益單位,輔助生產車間之間相互提供的產品和勞務,不互相分配費用。
採用直接分配法,由於各輔助生產費用只是進行對外分配,只分配一次,計算簡便。當輔助生產車間相互提供產品或勞務差異較大時,分配結果往往與實際不符。
適用範圍
這種分配方法只適用於在輔助生產內部相互提供產品或勞務不多、不進行費用的互動分配對輔助生產成本和產品生產成本影響不大的情況下採用。主要適用輔助生產車間之間不進行成本核算的小型企業。和輔助生產車間核算有困難的企業。
計算公式
其分配的計算公式為:
某種輔助生產費用分配率=該輔助生產車間費用總額÷基本生產車間和其他部門耗用勞務(或產品)總量
某車間、部門(或產品)應分配的輔助生產費用=該車間、部門(或產品)耗用勞務總量×輔助生產費用分配率
舉例分析
直接分配法案例
例:某企業設供汽和機修兩個輔助生產車間,供汽車間歸集入帳的費用合計為8600元,機修車間已歸集入帳的費用合計為2400元。假設供汽和機修兩個輔助生產車間發生的費用及提供的勞務數量如下表:
| 車間部門 | 供汽(噸) | 機修(工時) |
| 供汽車間 | 100 | |
| 機修車間 | 50 | |
| 基本生產車間 | 1200 | 620 |
| 行政管理部門 | 150 | 80 |
| 合計 | 1400 | 800 |
| 已歸集入賬的費用合計 | 8600(元) | 2400(元) |
根據上述資料,分別採用直接分配法和代數分配法編制的輔助生產費用分配表如下:表—1和表—2
輔助生產費用分配表:表—1(直接分配法)
| 生產車間 | 待分配的費用 | 分配數量 | 分配率 | 分配金額 | |||||
| 基本生產車間 | 管理部門 | 合計 | |||||||
| 數量 | 金額 | 數量 | 金額 | 數量 | 金額 | ||||
| 供汽車間 | 8600 | 1350 | 6.3704 | 1200 | 7644.48 | 150 | 955..52 | 1350 | 8600 |
| 機修車間 | 2400 | 700 | 3.4286 | 620 | 2125.73 | 80 | 274.27 | 700 | 2400 |
| 合計 | 11000 | 9770.21 | 1229.79 | 11000 | |||||
輔助生產費用分配表:表—2(代數分配法)
| 生產車間 | 單位成本 | 分配金額 | |||||||||
| 供汽車間 | 機修車間 | 基本生產車間 | 管理部門 | 合計 | |||||||
| 數量 | 金額 | 數量 | 金額 | 數量 | 金額 | 數量 | 金額 | 數量 | 金額 | ||
| 供汽車間 | 6.3857 | 50 | 319.28 | 1200 | 7662.84 | 150 | 957.85 | 1400 | 8939.97 | ||
| 機修車間 | 3.3391 | 100 | 339.91 | 620 | 2107.44 | 80 | 271.93 | 800 | 2719.28 | ||
| 合計 | 339.91 | 319.28 | 9770.28 | 1229.78 | 11659.25 | ||||||
從上表中的計算可看出,由於供汽和檢修彼此提供的產品或勞務而應負擔的輔助生產費用相差不大,結果是按兩種方法計算的分配給非輔助生產車間、部門及各受益單位的輔助生產費用數額相差也不大,但直接分配法計算過程比代數分配法簡單的多,所以,在沒有實現會計電算化的企業中,如果輔助生產車間相互提供的產品或勞務而應負擔的輔助生產費用相差不大,宜採用直接分配法分配輔助生產費用,這樣即可簡化計算過程,又不失正確性。
零空間分配
研究背景
基於可靠性、機動性和安全性等方面的考慮,現代飛行器多採用多操縱面冗餘布置形式,控制分配技術是解決操縱面冗餘飛行器控制的一種有效方法。直接分配法(Direct Allocation)是一種非常值得研究的控制分配方法,直接分配法具有兩個重要優點:一是直接分配法可以實現對可達轉矩集 100% 的分配;二是在轉矩指令不可達時,直接分配法可以保持轉矩指令的方向性。
直接分配法由 Durham 提出,Durham 對二維、三維轉矩分配問題及可達轉矩集邊界搜尋方法進行了研究。Petersen 和 Bodson 對直接分配法的計算效率及“控制共線” 問題進行了研究。Bolender 和 Doman給出了考慮舵效非線性的可達轉矩集。李衛琪提出了相鄰面搜尋算法,放寬了控制效率矩陣任意三列線性無關的限制條件;史靜平研究了共面系統以及可達轉矩集不包括原點系統的分配問題。雖已進行大量研究,但是直接分配法只能對指定方向上誤差最小目標進行最佳化的固有缺點仍未得到很好解決。為了使直接分配法可以對其他目標進行最佳化,Durham 進行了一些初步研究。Durham 的思路是將其他最佳化目標轉化為可達轉矩集的一維,將三維轉矩分配問題轉化為高維轉矩分配問題,但是高維可達轉矩集的求取難度較大以及幾何上的抽象性限制了這種方法的套用。研究利用零空間可對控制量進行調節的特性, 在三維轉矩分配的基礎上對零空間坐標K進行數學規劃,使控制量最小和阻力最小兩種目標達到最優。仿真結果表明,研究方法在保持了直接分配法原有優點的同時,可以實現控制量最小和阻力最小的控制分配。
基本原理
控制分配問題是指如何將控制律給出的期望控制指令分配給冗餘的操縱面,並使某些特定指標達到最優。飛控系統中,期望控制指令一般為三個軸上的操縱力矩。僅考慮操縱面的位置約束,假定操縱面舵偏與操縱力矩之間為線性關係。直接分配法是一種幾何算法,其重要理論基礎是可達轉矩集( Attainable Moment Set) 。可達轉矩集是指控制量在滿足約束的條件下,由控制量產生的所有轉矩的集合。對於m維空間中的控制量,由控制約束條件可確定受限控制集。給定控制效率矩陣,由線性映射即可確定 n 維空間中的可達轉矩集合。
研究結論
針對直接分配法不能對控制量、阻力等目標進行最佳化的缺點,給出了一種基於零空間的改進直接分配法,該方法通過零空間對直接分配法結果進行再調節使其他給定目標最優。由推導可知,控制量最小與阻力最小分別可以通過對坐標 K 的線性規劃與二次規劃實現。仿真結果表明,基於零空間的改進直接分配法在保持直接分配法原有優點的同時實現了對其他目標的最佳化。