預備知識
擾動
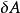 病態方程組
病態方程組 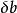 病態方程組
病態方程組 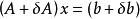 病態方程組
病態方程組 設方程組為Ax=b,係數矩陣A和常數向量b的擾動分別記為:和,則實際求解的方程組為。
條件數
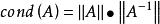 病態方程組
病態方程組 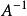 病態方程組
病態方程組 求解線性方程組Ax=b時,設A是n階非奇異矩陣,‖·‖為矩陣的任一種從屬範數,則 ,稱為矩陣A的條件數,其中 是A的逆矩陣。
定義
病態方程組是指因係數的很小改變卻導致解改變很大的方程組。病態的另外一個解釋是很大範圍的解都能近似滿足方程組。因為捨入誤差會使係數有一些小的改變,那么對於病態方程組,這些人為的改變會導致解有很大的誤差。
表述一
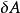 病態方程組
病態方程組 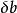 病態方程組
病態方程組 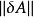 病態方程組
病態方程組 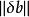 病態方程組
病態方程組 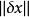 病態方程組
病態方程組 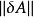 病態方程組
病態方程組 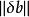 病態方程組
病態方程組 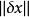 病態方程組
病態方程組 設方程組為Ax=b,係數矩陣A和常數向量b的擾動分別記為:和,如果和很小,而很大,則稱方程組Ax=b為病態(ill-conditioned)方程組,稱係數矩陣A為關於求解方程組或求逆的病態矩陣;反之,如果和微小時,也很微小,則稱方程組Ax=b為良態(well-conditioned)方程組,稱係數矩陣A為關於求解方程組或求逆的良態矩陣。病態方程組對任何算法都將產生數值不穩定性(如用LU分解法求解線性方程組時,更換主元有可能使解的精確度大大下降)。
表述二
求解線性方程組Ax=b時,設A是n階非奇異矩陣,當條件數Cond(A)比較大時,A和b的小擾動會引起解的較大誤差,所以條件數Cond(A)刻畫了方程組Ax=b的性態。如果條件數比較大,就說方程組是“病態”的;如果條件數比較小,就說方程組是“良態”的;當然,病態和良態是相對的。
典例
設有方程組:
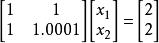 病態方程組
病態方程組 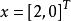 病態方程組
病態方程組 易得其精確解為 。
若常數項有一個擾動,得到方程組:
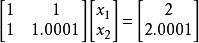 病態方程組
病態方程組 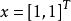 病態方程組
病態方程組 則其解為 。
可見A或b中元素的0.0001的微小變化會導致方程組解的巨大差異,這樣的方程組就是“病態”方程組,可以利用範數來描述向量和矩陣的擾動誤差。
判斷和發現
對於病態的線性方程組,其求解自然要難於良態的方程組,或要採取特殊的方法才能求出有用的解。在求解以前,怎樣判斷和發現Ax=b是病態的呢?
一般方法
根據病態方程組的定義,可以通過計算條件數來判斷。由於定義中涉及A ,故計算量太大而通常不被採用.人們經常利用的是估計條件數的方法。
特殊情況
在特殊情況下,可以依據下面出現的情況來判斷:
(1)當det(A)相對來說很小或者A的某些行(或列)近似線性相關時,Ax=b可能是病態的;
(2)如果用選主元消去法求解Ax=b,在A的約化過程中出現小的主元,Ax=b可能是病態的;
(3)當解Ax=b時出現一個很大的解,Ax=b可能是病態的;
(4)當係數矩陣A的元素數量級相差很大,並且無一定規則時,Ax=b可能是病態的。
四種處理原則
若發現Ax=b可能是病態的.通常有四種處理原則:
採用高精度的算術運算
如利用雙倍字長進行計算,以便改善和減輕矩陣病態的影響,但計算時間將大大增加。
採用預處理方法
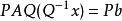 病態方程組
病態方程組 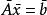 病態方程組
病態方程組 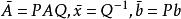 病態方程組
病態方程組 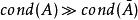 病態方程組
病態方程組 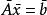 病態方程組
病態方程組 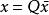 病態方程組
病態方程組 尋求非奇異矩陣P,Q,使求解Ax=b(設A為n維非奇異方陣)轉化為求解 或,其中 ,且改善A的條件數 。於是,可先求解 ,再求解 。當A為對稱正定矩陣時,一般選取P,Q為對角陣或三角陣。
對病態線性方程組Ax=b進行預處理,如取P,Q為對角陣,稱為平衡方法,即當係數矩陣A的元素數量級相差很大時,可採用行均衡或列均衡方法,這時矩陣A的條件數可能得到改善。所謂行均衡,是在解Ax=b之前,對A的每一行都乘以適當的數,使A所有的行按照某種範數大體上有相同的長度。
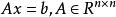 病態方程組
病態方程組 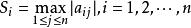 病態方程組
病態方程組 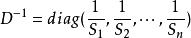 病態方程組
病態方程組 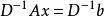 病態方程組
病態方程組 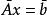 病態方程組
病態方程組 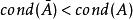 病態方程組
病態方程組 設 非奇異,計算 ,令 於是,求解Ax=b化為求解 或 ,這時有 。
採用特殊的數值解法
採用某些特殊的數值方法求解。
找病因改問題
尋找出現病態的原因,改變原問題的提法。

