簡單理解
如果我們把一隻貓關進一個密閉的盒子,用槍對盒子射擊,這支槍的扳機是由原子衰變扣動的,那么我們便無法知道這隻貓究竟是死還是活,因為原子的是否衰變是一個隨機事件。在量子力學中,我們便把這隻貓所處的狀態稱為死與活的疊加狀態。
物理意義
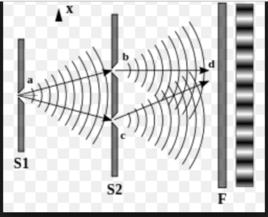
當我們進行單個電子的雙縫干涉實驗時,兩條狹縫上都留下了這個電子干涉過的條紋。一旦我們用專門的儀器觀察電子進行,干涉條紋便消失了。對此的解釋是這樣的:當我們不進行觀察時,電子具有波動性,因此能彌散開來,留下條紋;一旦我們展開觀察,就有一個光子撞擊了這個電子,這個電子便具有了確定的位置,呈現出粒子性,直線傳播而無法干涉這兩條狹縫。在不觀察時,由於電子沒有確定的位置,電子便是在各種位置的疊加狀態,而人的觀察使得這個電子退出了疊加狀態。
量子力學認為微觀事物的運動和狀態均是不確定的,如果將其推廣到巨觀世界上來,那么,即將擲出的骰子、猶豫不決的人、風暴的移動方向等各種不確定的事物均可以被認為是處在多種狀態的疊加狀態。在平行宇宙理論中,一個處在疊加狀態的物質可以分裂,不同的狀態發生在不同的宇宙之中。
態疊加原理
在量子力學裡, 態疊加原理(superposition principle)表明,假若一個量子系統的量子態可以是幾種不同量子態中的任意一種,則它們的歸一化線性組合也可以是其量子態。稱這線性組合為“疊加態”。假設組成疊加態的幾種量子態相互正交,則這量子系統處於其中任意量子態的機率是對應權值的絕對值平方。
從數學表述,態疊加原理是薛丁格方程的解所具有的性質。由於薛丁格方程是個線性方程,任意幾個解的線性組合也是解。這些形成線性組合(稱為“疊加態”)的解時常會被設定為相互正交(稱為“基底態”),例如氫原子的電子能級態;換句話說,這幾個基底態彼此之間不會出現重疊。這樣,對於疊加態測量任意可觀察量所得到的期望值,是對於每一個基底態測量同樣可觀察量所得到的期望值,乘以疊加態處於對應基底態的機率之後,所有乘積的總和。
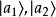 疊加態
疊加態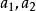 疊加態
疊加態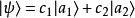 疊加態
疊加態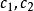 疊加態
疊加態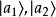 疊加態
疊加態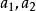 疊加態
疊加態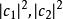 疊加態
疊加態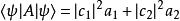 疊加態
疊加態更具體地說明,假設對於某量子系統測量可觀察量A,而可觀察量A的本徵態分別擁有本徵值,則根據薛丁格方程的線性關係,疊加態也可以是這量子系統的量子態;其中,分別為疊加態處於本徵態的機率幅。假設對這疊加態系統測量可觀察量A,則測量獲得數值是的機率分別為,期望值為。