鑽石魔方
異型魔方圖鑑原名Skewb Diamond，是一種具有八面體結構的魔方。所有的塊都可以和相鄰塊一起移動。它總共有十四個可移動的塊，形成138240種變化狀態。
六色五魔方
異型魔方五魔方，原名為Megaminx。是一種十二面體魔方，總共有12箇中心片，20個角片和30個邊片，所以總共有50塊可以移動的部分。每箇中心都有一種顏色。邊片則有兩種顏色，角片則有三種。每個面上都有一個中心片，角片邊片各五個。同時也是世界魔方協會承認和指定的比賽項目之一。
金字塔魔方
異型魔方金字塔魔方（Pyraminx）一種四面體魔方。它是由Uwe Meffert發明的，在他自己的魔方網站Mefferts商店進行銷售。有四個外角塊、四個內角塊和六個邊塊。通過鏇轉可以改變其顏色排列。軸鏇轉塊可以鏇轉後而狀態不改變。6個邊塊則可以自由鏇轉。而四個頂塊可以獨立於其他塊進行自我鏇轉。
粽子魔方
粽子魔方粽子魔方（英文名稱：Mastermorphix）是由普通三階改裝而來，是六軸的結構。粽子魔方
解法
粽子魔方確實是三階魔方，關鍵是要把角塊、棱塊、中心塊分辨出來。
先試著轉動粽子，然後分清“層”。
中心塊在每一層中間，不同於普通三階的地方是，中心塊有兩個面。
棱塊緊緊圍繞在中心塊四周，只有一個面。
角塊有兩種，一種是四個頂角，有三個面；另外是四個小三角形的塊，只有一面。
這時候再來還原，應該就不至於一頭霧水了。
粽子可以不考慮顏色的問題，所以有些步驟是可以簡化的。但同時金銀粽子魔方的中心塊和棱塊有方向，角塊反而沒有方向了。（四色粽子中心塊有兩個面，棱塊只有一個面，角塊一半有三個面，一半有一個面）這又增加了一些難度。
觀察——粽子魔方的觀察將顯得非常之難，潛力非常大。究竟用哪一面做底面，就看你觀察的功力了。
Cross——不需要考慮顏色，只需考慮底棱方向和中層四個中心塊的方向問題。
F2L ——不需考慮顏色，考慮中棱方向問題。
OPLL——我還有點暈，棱塊方向不對究竟算OLL，還是PLL呢？
講幾個小發現吧：
1. 頂層鄰棱反向公式：
(R U R' U')×2 注意：R是在兩棱中靠左的那層做。
這個是在頂層復原的時候用的，如果有兩個鄰棱需要調整方向，用這個公式。對棱調整方向的我還沒想明白呢。
補充：
舉個例子吧， UR和UB 方向不對，就用R U R' U' R U R' U'
UF和UR方向不對，就用F U F' U' F U F' U'
其實最後一步U 和 U'效果是一樣的。如果是復原最終狀態。
2. 相鄰兩個中心塊反向：
這種情況先做個三棱換公式，再做 (R U R' U')即可完成。
暫時還沒找到簡化公式，煩勞其他大俠指教。
3. 單箇中心塊反向：
R U' R' U' y' R U R
R U' R' U' y' R U R'
在沒找出簡化公式前，我曾經用過的笨辦法：
a. 用兩次三角換把兩組鄰角對換，再用兩次鄰棱反向公式把兩組鄰棱對換；
b. 做一次R U' R'，撥U2 再做（R U R' U'）×2 調整棱塊方向，再做逆時針三角換公式復原。
4. 以三角換公式為例：
順時針開頭的（R2 D2）、逆時針結尾的（D2 R2）有可能是廢步，
另一種情況下，兩公式中的（R D2 R'）有可能是廢步，
公式像是被簡化了。
5. 對棱反向（或對棱換）
M U M U M U2 M' U M' U M' U2 就行，而且最後的U2是廢步，不需要了。
暫時還沒最佳化，應該有更簡潔的公式。
粽子魔方尤其是單色粽子（只需復原形狀）應該有其單獨的解法系統和公式，估計角先和棱先有很大的空間。希望廣大魔友共同探討。
三角翻公式也可以調鄰棱方向：
R' U' R U' R' U2 R
不過這個公式起手是在兩棱中靠右的那層做。
蛇形魔方
為長型的魔方，又稱長條魔方。
鏡面魔方
異型魔方鏡面的意思是，表面的銀色貼紙可以反光，看起來像是鏡子，由此得名。看著鏡面魔方雖然形狀怪異，但是只要會還原三階魔方的，自己只要觀察幾分鐘，你就會得到要領，很快就可以搞定啦。而在還原的過程中，Mirror魔方會呈現千變萬化的炫酷形狀，也可做擺設！
魔球魔方
異型魔方data-layout="right" 名稱為Magic Ball，為球形，但是基本上是2階的結構。球型魔方的泛稱，最常見的包括球形3階，球形2階（如魯比克地球儀魔方）等。迪士尼四軸球，Orbix，Meffert's 3-D Creative Puzzle Ball，Meffert's 12Color Impossiball Special等也屬於球型魔方的範疇。另外，一些球型滑塊智力玩具如凡太奇球，Rubik's brain racker等也被稱之為魔球。
斜轉魔方
斜轉魔方也叫做斜轉方塊，是一種魔方風格的機械智力玩具。由托尼·達勒姆發明，由烏韋·梅弗特（Uwe Meffert）銷售。雖然它是一個立方體，它不同於魔方的架構，它的鏇轉軸穿過立方體的每個角落，而不是每個面的中心。斜轉方塊一共有四個軸，每一個軸是一個立體對角線。因此，每個動作都會影響所有六個面。 梅弗特原本稱這個玩具作“金字塔立方”，強調這是金字塔魔方系列的一部分。 他也發明了高階斜轉方塊，例如大師斜方和優秀斜方。
異型魔方
斜轉魔方內部結構Square 1
異型魔方Square 1，原稱Back to Square One，是魯比克魔方系列之一，是由Karel Hrsel和Vojtech Kopsky在1992年共同發明的。它與其他魔方很大的不同點就是在轉動的時候會改變形狀，這也是它擁有非凡難度和魅力的原因之一。
亞歷山大之星
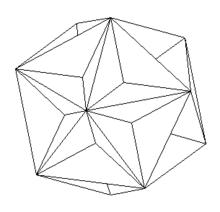亞歷山大之星運動狀態
異型魔方亞歷山大 之星（Alexander's Star），亞當·亞歷山大於1982年發明的益智玩具，並於1985年獲得了專利。是一個有30塊可移動部分的正十二面體形狀的魔方。可以讓五塊一組的星型環繞最外側頂點鏇轉。這個玩具的挑戰是讓它達到每個星形五個相同顏色的面環繞，對面的星形也被同一顏色環繞的狀態。
