基本內容
玫瑰線玫瑰線的說法源於歐洲海圖。在中世紀的航海地圖上,並沒有經緯線,有的只是一些從中心有序地向外輻射的互相交叉的直線方向線。此線也稱羅盤線,希臘神話里的各路風神被精心描繪在這些線上,作為方向的記號。所以,哥倫布探險隊中的西班牙水手想到方向的時候,並不是羅盤方位上的多少度,而是風(losvientos)。而葡萄牙水手則稱他們的羅盤盤面為風的玫瑰(rosedosventor)。水手們根據太陽的位置估計風向,再與“風玫瑰”對比找出航向。玫瑰線,即指引方向的線。
世界上第一個明確提出經緯度理論的人是古希臘學者托勒密。最早的本初子午線則出現在15世紀出版的托勒密的世界地圖上,定在了當時人們心中的世界起點,即現大西洋中非洲西北海岸附近的加那利群島。
不像緯線有長 有短,所有經線的長度皆相同,人們可以選擇通過地球上任何一點的經線作為起始線。於是,在過去的許多年裡,每個國家出版的地圖所用經度皆是由自己的起始經線進行推算的,而航海家們使用的航海地圖又往往是採用某一航線的出發點作為起算點。巴黎零度經線的設立比格林尼治線要早,不過無論是巴黎經線還是格林尼治經線,這些零度經線的劃定都是主觀的劃定。
1569年,墨卡托發明了航海圖沿用至今的投影,不過繪有經緯網的世界地圖30年後才得以出版,零度經線設在大西洋上的亞速爾群島。那時英國所使用的航海圖,零度經線也設在亞速爾群島,1676年改為倫敦,最初定點在聖?保羅大教堂,後定點在格林尼治天文台。在法國,紅衣主教里舍利厄1634年選中了通過加那利群島最西邊的耶魯島的經線作為零度經線,1667年巴黎天文台建立,零度經線改為通過巴黎的經線。17世紀的荷蘭地圖上,零度經線是阿姆斯特丹威斯特教堂的南北軸。西班牙以西、葡分界的教皇子午線為零度經線。義大利地圖上使用的零度經線位於羅馬。在中國,清康熙四十八年,清政府確定了京城中軸線為零度經線。
當精確測定經度成為航海的關鍵問題後,1675年,英國在倫敦附近建立了格林尼治天文台,並第一個研究出了簡易測定航海中船舶方位的方法。1767年,根據格林尼治天文台提供的數據繪製的英國航海曆出版,這份航海曆上的零度經線就是通過格林尼治天文台的經線。這個時候的英國,已是頭號海上強國。
1850年,美國政府決定在航海圖中採用格林尼治子午線取代通過華盛頓的零度經線作為本初子午線。1853年,俄國海軍宣布不再使用普爾可夫天文台(今列寧格勒附近)的零度經線編制航海曆,而採用格林尼治子午線為本初子午線。到了1883年,可以說除了法國編制的地圖,其餘國家的地圖幾乎都是採用格林尼治經線作為零度經線。
1884年,國際子午線會議在美國華盛頓召開,通過決議把經過格林尼治的經線正式確定為零度經線、世界時間計量和經度計量的標準子午線――本初子午線。不過法國人並不服氣這個決議,在自己國家發行的地圖上,仍將本初子午線定在首都巴黎,直到1911年後才改為格林尼治線。可見,對於事實,大家並不一定有共識,而是依賴自己的觀點而定.
數學中的
玫瑰線方程及其幾何結構
玫瑰線的極坐標方程為:ρ=a* sin(nθ),ρ=a*cos(nθ)
用直角坐標方程表示為: x=a* sin(nθ)* cos(θ), y=a*sin(nθ)* sin(θ)
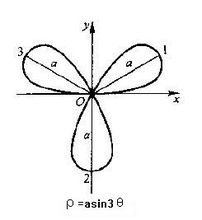 三葉玫瑰線
三葉玫瑰線根據三角函式的特性可知,玫瑰線是一種具有周期性且包絡線為圓弧的曲線,曲線的幾何結構取決於方程參數的取值,不同的參數決定了玫瑰線的大小、葉子的數目和周期的可變性。這裡參數a(包絡半徑)控制
葉子的長短,參數n控制葉子的個數、葉子的大小及周期的長短。
如對於方程式ρ=5* sin(3*θ)、ρ=5* sin(2*θ)、ρ=5* sin(3*θ/2),分別對應的是三葉、四葉和六葉玫瑰線。
玫瑰線的參數特性
玫瑰線的參數主要是a、n及θ,其值的大小決定玫瑰線的形狀,包括葉子數、葉子長度寬度和曲線閉合周期。係數a只跟葉子的長度有關,而n和θ則影響玫瑰線的多樣性和周期性,本文主要討論n和θ對玫瑰線幾何結構的影響,從而揭示玫瑰線的生成規則。通過計算機對方程式ρ=a* sin(nθ)的大量試驗,證明玫瑰線具有如下三個特性:
特性1當n為整數時,若n為奇數,則玫瑰線的葉子數為n,閉合周期為π,即θ角在0-π內玫瑰線是閉合的。當n為偶數時,玫瑰線的葉子數為2n,閉合周期為2π,即θ角取值在0-2π內玫瑰線才是閉合和完整的。
特性2當n為非整數的有理數時,設為L/W,且L/W為簡約分數,此時,L與W不可能同時為偶數。L決定玫瑰線的葉子數,W決定玫瑰線的閉合周期(Wπ或2Wπ,見特性3)及葉子的寬度,W越大,葉子越寬。但W也會同時影響葉子數的多少,對同一奇數值L,在W分別取奇數和偶數值時,葉子數也是不同的。
特性3當L或W中有一個為偶數時,玫瑰線的葉子數為2L,閉合周期為2Wπ。當L或W同為奇數時,玫瑰線的葉子數為L,閉合周期為Wπ。換句話說,生成偶數個葉子的玫瑰線, L或W中必須有且只有一個為偶數值,且L為葉子數的一半,而生成奇數個葉子的玫瑰線, L和W都必須為奇數,且L值就是葉子數。
玫瑰線的生成規則
 玫瑰線
玫瑰線對於給定葉子數的玫瑰線,可以通過選擇n或L/W不同形式來生成。
相關條目
百福郡華人聯誼會
長春市第二實驗國小
格林威治華人協會
東四五條
中國社會科學院法學研究所
厄普頓·辛克萊
法證先鋒

